题目内容
下列直线中,与直线x-2y+1=0垂直的是( )
| A、2x-y-3=0 |
| B、x-2y+3=0 |
| C、2x+y+5=0 |
| D、x+2y-5=0 |
考点:直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:分别求出五条直线的斜率,由斜率互为负倒数求得答案.
解答:
解:直线直线x-2y+1=0的斜率为
,
而直线2x-y-3=0的斜率为2,
x-2y+3=0的斜率为
,
2x+y+5=0的斜率为-2,
x+2y-5=0的斜率为-
.
∴与直线x-2y+1=0垂直的是2x+y+5=0.
故选:C.
| 1 |
| 2 |
而直线2x-y-3=0的斜率为2,
x-2y+3=0的斜率为
| 1 |
| 2 |
2x+y+5=0的斜率为-2,
x+2y-5=0的斜率为-
| 1 |
| 2 |
∴与直线x-2y+1=0垂直的是2x+y+5=0.
故选:C.
点评:本题考查了直线的一般式方程与直线垂直的关系,考查了两直线垂直与斜率间的关系,是基础题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
已知两点A(1,0),B(-1,
),O为坐标原点,点C在第二象限,且∠AOC=135°,设
=-
+λ
(λ∈R),则实数λ等于( )
| 3 |
| OC |
| OA |
| OB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列命题中是假命题的是( )
| A、?α、β∈R,使sin(α+β)=sinα+sinβ |
| B、?a>0,函数f(x)=ln2x+lnx-a有零点 |
| C、?ϕ∈R,函数f(x)=sin(2x+ϕ)都不是偶函数 |
| D、?m∈R,使f(x)=(m-1)•xm2-4m+3是幂函数,且在(0,+∞)上单调递减 |
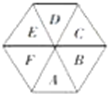 在一个正六边形的六个区域栽种观赏植物(如图),要求同一块中种同一种植物,相邻的两块种不同的植物.
在一个正六边形的六个区域栽种观赏植物(如图),要求同一块中种同一种植物,相邻的两块种不同的植物.(1)现有2种不同的植物可供选择,则有种栽
(2)现有4种不同的植物可供选择,则有
下列角中,终边在y轴正半轴上的是( )
A、
| ||
B、
| ||
| C、π | ||
D、
|
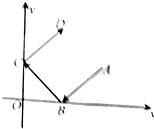 如图所示,光线从点A(2,1)出发,到x轴上的点 B后,被x轴反射到y轴上的
如图所示,光线从点A(2,1)出发,到x轴上的点 B后,被x轴反射到y轴上的