题目内容
已知集合M={y|y=3-x2，x∈R}，N={x|y=
}，则M∩（∁UN）=（ ）
(
|
| A、（-∞，0） | B、[0，3） |
| C、（0，3] | D、∅ |
考点：交、并、补集的混合运算
专题：集合
分析：求出集合M，N，根据集合的基本运算进行求解即可．
解答：
解：M={y|y=3-x2，x∈R}={y|y≤3}，N={x|y=
}={x|x≤0}，
则∁UN={x|x＞0}，
即M∩（∁UN）={x|0＜x≤3}，
故选：C
(
|
则∁UN={x|x＞0}，
即M∩（∁UN）={x|0＜x≤3}，
故选：C
点评：本题主要考查集合的基本运算，求出集合M，N的等价条件是解决本题的关键．
练习册系列答案
相关题目
命题“?x0∈R，使得2x0≤4”的否定是（ ）
| A、?x∈R，使得2x＞4 |
| B、?x0∈R，使得2x0≥4 |
| C、?x∈R，使得2x＜4 |
| D、?x0∈R，使得2x0＞4 |
已知两点A（1，0），B（-1，
），O为坐标原点，点C在第二象限，且∠AOC=135°，设
=-
+λ
（λ∈R），则实数λ等于（ ）
| 3 |
| OC |
| OA |
| OB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
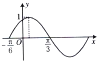函数f（x）=sin（ωx+φ）（x∈R）（ω＞0，|φ|＜| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
与圆x2+（y+5）2=9相切，且在两坐标轴上截距相等的直线共有（ ）条．
| A、2 | B、3 | C、4 | D、6 |
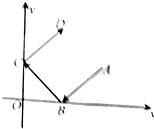如图所示，光线从点A（2，1）出发，到x轴上的点 B后，被x轴反射到y轴上的