题目内容
已知α为第二象限角,sinα=
,则sin(π+2α)=( )
| 4 |
| 5 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
考点:二倍角的正弦,运用诱导公式化简求值
专题:三角函数的求值
分析:由α为第二象限角及sinα的值,利用同角三角函数间的基本关系求出cosα的值,原式利用诱导公式化简后,再利用二倍角的正弦函数公式化简,将各自的值代入计算即可求出值.
解答:
解:∵α为第二象限角,sinα=
,
∴cosα=-
=-
,
则原式=-sin2α=-2sinαcosα=
.
故选:C.
| 4 |
| 5 |
∴cosα=-
| 1-sin2α |
| 3 |
| 5 |
则原式=-sin2α=-2sinαcosα=
| 12 |
| 25 |
故选:C.
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
命题:“若x>1,则lnx>0”的否命题为( )
| A、若x>1,则lnx≤0 |
| B、若x≤1,则lnx>0 |
| C、若x≤1,则lnx≤0 |
| D、若lnx>1,则x>0 |
下列角中,终边在y轴正半轴上的是( )
A、
| ||
B、
| ||
| C、π | ||
D、
|
i是虚数单位,
=( )
| i |
| -1+i |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
已知命题p:?x<0,x2>0,那么¬p是( )
| A、?x≥0,x2≤0 |
| B、?x≥0,x2≤0 |
| C、?x<0,x2≤0 |
| D、?x≥0,x2≤0 |
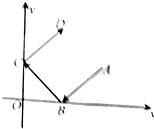 如图所示,光线从点A(2,1)出发,到x轴上的点 B后,被x轴反射到y轴上的
如图所示,光线从点A(2,1)出发,到x轴上的点 B后,被x轴反射到y轴上的