题目内容
有2个兴趣小组,甲、乙、丙三位同学各参加其中一个小组,每位同学参加各个小组的可能性相同.则这三位同学参加同一个兴趣小组的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:相互独立事件的概率乘法公式
专题:计算题,概率与统计
分析:本题是一个古典概型,试验发生包含的事件数是2×2×2=8种结果,满足条件的事件是这三位同学参加同一个兴趣小组有2种结果,根据古典概型概率公式得到结果.
解答:
解:由题意知本题是一个古典概型,试验发生包含的事件数是2×2×2=8种结果,
满足条件的事件是这三位同学参加同一个兴趣小组,由于共有2个小组,则有2种结果,
根据古典概型概率公式得到P=
=
,
故选A.
满足条件的事件是这三位同学参加同一个兴趣小组,由于共有2个小组,则有2种结果,
根据古典概型概率公式得到P=
| 2 |
| 8 |
| 1 |
| 4 |
故选A.
点评:本题考查古典概型概率公式,是一个基础题,确定试验发生包含的事件数和满足条件的事件数是关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
与圆x2+(y+5)2=9相切,且在两坐标轴上截距相等的直线共有( )条.
| A、2 | B、3 | C、4 | D、6 |
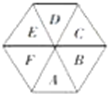 在一个正六边形的六个区域栽种观赏植物(如图),要求同一块中种同一种植物,相邻的两块种不同的植物.
在一个正六边形的六个区域栽种观赏植物(如图),要求同一块中种同一种植物,相邻的两块种不同的植物.(1)现有2种不同的植物可供选择,则有种栽
(2)现有4种不同的植物可供选择,则有
“a>b”是“a+1>b”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
命题:“若x>1,则lnx>0”的否命题为( )
| A、若x>1,则lnx≤0 |
| B、若x≤1,则lnx>0 |
| C、若x≤1,则lnx≤0 |
| D、若lnx>1,则x>0 |
i是虚数单位,
=( )
| i |
| -1+i |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
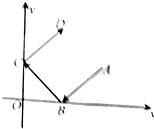 如图所示,光线从点A(2,1)出发,到x轴上的点 B后,被x轴反射到y轴上的
如图所示,光线从点A(2,1)出发,到x轴上的点 B后,被x轴反射到y轴上的