题目内容
证明：f（x）=x2-2x在区间（1，+∞）上递增．
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：根据单调性的定义证明即可．
解答：
证明：取任意的x1＜x2∈（1，+∞），
∴f(x1)-f(x2)=x12-2x1-(x22-2x2)，
=x12-2x1-x22+2x2，
=（x12-x22）-2（x1-x2），
=（x1+x2）（x1-x2）-2（x1-x2），
=（x1-x2）（x1+x2-2），
∵x1＜x2∈（1，+∞），
∴x1-x2＜0，x1+x2-2＞0
∴f（x1）-f（x2）＜0，
即f（x1）＜f（x2），
∴f（x）=x2-2x在区间（1，+∞）上递增．
∴f(x1)-f(x2)=x12-2x1-(x22-2x2)，
=x12-2x1-x22+2x2，
=（x12-x22）-2（x1-x2），
=（x1+x2）（x1-x2）-2（x1-x2），
=（x1-x2）（x1+x2-2），
∵x1＜x2∈（1，+∞），
∴x1-x2＜0，x1+x2-2＞0
∴f（x1）-f（x2）＜0，
即f（x1）＜f（x2），
∴f（x）=x2-2x在区间（1，+∞）上递增．
点评：本题主要考查了函数的单调性用定义证明的方法，注意计算和判断符号，属于基础题．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
相关题目
物体自由落体运动方程为s（t）=
gt2，若
=g=9.8m/s，那么下面说法正确的是（ ）
| 1 |
| 2 |
| lim |
| n→∞ |
| s(1+△t)-s(1) |
| △t |
| A、9.8m/s是0～1s这段时间内的平均速度 |
| B、9.8m/s是从1s到（1+△t）s这段时间内的速度 |
| C、9.8m/s是物体在t=1s这一时刻的速度 |
| D、9.8m/s是物体从1s到（1+△t）s这段时间内的平均速度 |
如果圆柱的轴截面周长为定值4，则圆柱体积的最大值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
常说“便宜没好货”，这句话的意思是：“不便宜”是“好货”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知x，y之间的数据如下表所示，则y与x之间的线性回归方程必过点（ ）
| x | 1.08 | 1.12 | 1.19 | 1.30 |
| y | 2.25 | 2.37 | 2.40 | 2.60 |
| A、（0，0） |
| B、（1.17，0） |
| C、（0，2.41） |
| D、（1.17，2.41） |
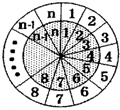如图所示的两个同心圆盘均被n等分（n∈N+且n≥2），在相重叠的扇形格中依次同时填上1，2，3，L，n，内圆盘可绕圆心旋转，每次可旋转一个扇形格，当内圆盘旋转到某一位置时，定义所有重叠扇形格中两数之积的和为此位置的“旋转和”．
读该程序图（其中x满足：0＜x＜12）