题目内容
已知函数f(x)=(x2+2x)e-x,x∈R.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若f′(x)>1,求证:f(x)<1.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若f′(x)>1,求证:f(x)<1.
考点:利用导数研究函数的单调性,导数的运算
专题:导数的综合应用
分析:(1)利用导数即可求得函数的单调区间;
(2)由f′(x)>1得(2-x2)e-x>1,即ex<2-x2,等价于x2+x-1<x+1-ex,
先证:x+1≤ex,令g(x)=ex-(x+1),利用导数即可证得g(x)≥g(0)=0,即x+1≤ex,变形即可证得结论成立.
(2)由f′(x)>1得(2-x2)e-x>1,即ex<2-x2,等价于x2+x-1<x+1-ex,
先证:x+1≤ex,令g(x)=ex-(x+1),利用导数即可证得g(x)≥g(0)=0,即x+1≤ex,变形即可证得结论成立.
解答:
解:(1)∵f(x)=(x2+2x)e-x,x∈R,
∴f′(x)=(2x+2)e-x-(x2+2x)e-x=(2-x2)e-x,
∴由f′(x)>0得-
<x<
,故f(x)在(-
,
)上是增函数,
由f′(x)<0得x<-
或x>
,故f(x)在(-∞,-
),(
,+∞)上是减函数.
(2)由f′(x)>1得(2-x2)e-x>1,即ex<2-x2,等价于x2+x-1<x+1-ex,
先证:x+1≤ex,令g(x)=ex-(x+1),有g′(x)=ex-1,
当x>0时,g′(x)>0,g(x)在(0,+∞)上单调递增;
当x<0时,g′(x)<0,g(x)在(-∞,0)上单调递减;
∴g(x)≥g(0)=0,即x+1≤ex,
∴x2+x-1<x+1-ex≤0,
∴x2+x-1<0,由此得x2+2x<x+1,
∴x2+2x<x+1≤ex,
∴(x2+2x)e-x<1,
即f(x)<1.
∴f′(x)=(2x+2)e-x-(x2+2x)e-x=(2-x2)e-x,
∴由f′(x)>0得-
| 2 |
| 2 |
| 2 |
| 2 |
由f′(x)<0得x<-
| 2 |
| 2 |
| 2 |
| 2 |
(2)由f′(x)>1得(2-x2)e-x>1,即ex<2-x2,等价于x2+x-1<x+1-ex,
先证:x+1≤ex,令g(x)=ex-(x+1),有g′(x)=ex-1,
当x>0时,g′(x)>0,g(x)在(0,+∞)上单调递增;
当x<0时,g′(x)<0,g(x)在(-∞,0)上单调递减;
∴g(x)≥g(0)=0,即x+1≤ex,
∴x2+x-1<x+1-ex≤0,
∴x2+x-1<0,由此得x2+2x<x+1,
∴x2+2x<x+1≤ex,
∴(x2+2x)e-x<1,
即f(x)<1.
点评:本题主要考查利用导数判断函数的单调性及求函数最值问题,以及利用导数证明不等式成立问题,注意问题的转化划归,属中档题.

练习册系列答案
相关题目
已知集合A={x|m+1≤x≤2m},B={x|log2x≤3},当A∩B=∅时,实数m的取值范围是( )
| A、1<m<7 |
| B、m<1或m>7 |
| C、0≤m<7 |
| D、m≤0或m>7 |
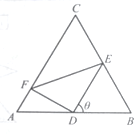 如图,正三角形ABC的边长为2,D、E、F分别在三边AB,BC和CA上,且D为AB的中点,∠EDF=90°,∠BDE=θ(0°<θ<90°).
如图,正三角形ABC的边长为2,D、E、F分别在三边AB,BC和CA上,且D为AB的中点,∠EDF=90°,∠BDE=θ(0°<θ<90°).