题目内容
3.设集合A={x|x2+2x-3>0},B={x|x2-2ax-1≤0,a>0},若A∩B中恰有一个整数,则实数a的取值范围是( )| A. | (0,$\frac{3}{4}$) | B. | [$\frac{3}{4}$,$\frac{4}{3}$) | C. | $[\frac{3}{4},+∞)$ | D. | (1,+∞) |
分析 先化简A,B,求集合A∩B,利用A∩B中恰含有一个整数,即可求实数a的取值范围.
解答 解:由A中不等式变形得:(x-1)(x+3)>0,
解得:x<-3或x>1,即A={x|x<-3或x>1},
函数y=f(x)=x2-2ax-1的对称轴为x=a>0,f(-3)=6a+8>0,
如图示: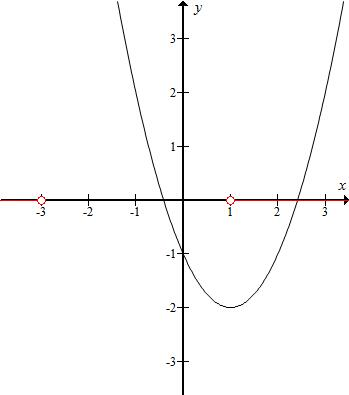
由对称性可得,要使A∩B恰有一个整数,
即这个整数解为2,
∴f(2)≤0且f(3)>0,
即 $\left\{\begin{array}{l}{4-4a-1≤0}\\{9-6a-1>0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a≥\frac{3}{4}}\\{a<\frac{4}{3}}\end{array}\right.$,
即$\frac{3}{4}$≤a<$\frac{4}{3}$,
故选:B.
点评 本题主要考查集合关系的应用,利用不等式和函数之间的关系,将不等式转化为函数,利用函数根的分布确定函数满足的条件是解决本题的关键,综合性较强,难度较大.

练习册系列答案
相关题目
18.仔细观察下面○和●的排列规律:○●○○●○○○●○○○○●○○○○○●○○○○○○●…
若依此规律继续下去,得到一系列的○和●,那么在前150个○和●中,●的个数是( )
若依此规律继续下去,得到一系列的○和●,那么在前150个○和●中,●的个数是( )
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
19.如图,在直角坐标系内,射线OT落在60°的终边上,任作一条射线OA,则射线落在∠xOT内的概率是( )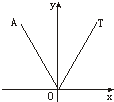

| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | 以上全不对 |
16.已知a=($\sqrt{2}$)-1,b=log23,c=lne,则a,b,c的大小关系为( )
| A. | a<b<c | B. | a<c<b | C. | c<b<a | D. | c<a<b |
13.双曲线$\frac{x^2}{5}$-$\frac{{y{\;}^2}}{4}$=1的焦点坐标为( )
| A. | (3,0)和(-3,0) | B. | (2,0)和(-2,0) | C. | (0,3)和(0,-3) | D. | (0,2)和(0,-2) |
