题目内容
14.如果p1•p2=4(q1+q2),证明关于x的二次方程x2+p1x+q1=0,x2+p2x+q2=0中至少有一个方程有实根.分析 至少有一个方程有实根的对立面是两个方程都没有根,由于正面解决此问题分类较多,而其对立面情况单一,故求解此类问题一般先假设所有方程都有实数根,然后由根的判别式解得方程都没有实数根的a的取值范围,其补集即为方程x2+p1x+q1=0与方程x2+p2x+q2=0中至少有一个方程有实数根,此种方法称为反证法.
解答 证明:假设原命题不成立,
即x2+p1x+q1=0与x2+p2x+q2=0都无实根.
∴△1=p12-4q1<0,△2=p22-4q2<0
两式相加得:
p12+p22-4q1-4q2<0,即p12+p22<4(q1+q2)
又∵p1p2=4(q1+q2),∴p12+p22<p1p2
即:(p1-$\frac{1}{2}$p2)2+$\frac{3}{4}$p22<0,此式显然不成立.
故假设不成立,原命题是正确的.
点评 本题考查反证法,解题时要合理地运用反证法的思想灵活转化问题,以达到简化解题的目的,在求解如本题这类存在性问题时,若发现正面的求解分类较繁,而其对立面情况较少,不妨如本题采取求其反而成立时的参数的取值范围,然后求此范围的补集,即得所求范围,本题中二个方程都是一元二次方程,故求解时注意根的判别式的运用.

练习册系列答案
相关题目
2.若a=30.3,b=(0.3)2,c=log30.2,则a,b,c的大小关系是( )
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | c<a<b |
19.如图,在直角坐标系内,射线OT落在60°的终边上,任作一条射线OA,则射线落在∠xOT内的概率是( )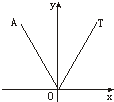

| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | 以上全不对 |