题目内容
11.有一休闲广场东侧建造一座钟楼,顶部嵌入一座大型时钟,钟面中心O距离地面30米,时钟分钟OP(P为分针末端)长8米,该挂钟于6月1日0点分开始揭幕启动.记经过t分钟时P距离地面的高度为h(t)米.(Ⅰ)求h(t)的函数解析式;
(Ⅱ)求启动后1小时内,h=26,t为何值.
分析 (Ⅰ)设h(t)的函数解析式为h(t)=Asin(ωt+θ)+B,利用条件求出参数,即可求h(t)的函数解析式;
(Ⅱ)8cos($\frac{π}{30}$t)+30=26,cos($\frac{π}{30}$t)=-$\frac{1}{2}$,即可求启动后1小时内,h=26,t为何值.
解答 解:(Ⅰ)设h(t)的函数解析式为h(t)=Asin(ωt+θ)+B,则$\left\{\begin{array}{l}{A+B=38}\\{-A+B=22}\end{array}\right.$,∴A=8,B=30;
∵T=$\frac{2π}{ω}$=60,∴ω=$\frac{π}{30}$.
t=0时,h(0)=8sinθ+30=38,∴θ=$\frac{π}{2}$,
∴h(t)=8sin($\frac{π}{30}$t+$\frac{π}{2}$)+30=8cos($\frac{π}{30}$t)+30;
(Ⅱ)8cos($\frac{π}{30}$t)+30=26,∴cos($\frac{π}{30}$t)=-$\frac{1}{2}$,
∵0≤t≤60,∴t=20或40分钟.
点评 本题考查三角函数模型的运用,考查学生的计算能力,正确建立函数模型是关键.

练习册系列答案
相关题目
2.若a=30.3,b=(0.3)2,c=log30.2,则a,b,c的大小关系是( )
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | c<a<b |
19.如图,在直角坐标系内,射线OT落在60°的终边上,任作一条射线OA,则射线落在∠xOT内的概率是( )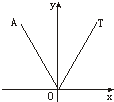

| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | 以上全不对 |
16.已知a=($\sqrt{2}$)-1,b=log23,c=lne,则a,b,c的大小关系为( )
| A. | a<b<c | B. | a<c<b | C. | c<b<a | D. | c<a<b |
16.曲线y=xex+1在点(1,e+1)处的切线方程是( )
| A. | 2ex-y-e+1=0 | B. | 2ey-x+e+1=0 | C. | 2ex+y-e+1=0 | D. | 2ey+x-e+1=0 |
 如图,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,点D是AB的中点.
如图,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,点D是AB的中点.