题目内容
4.已知函数f(x)=mx3-3mx2(m∈R,m≠0).(Ⅰ)求函数f(x)的单调增区间;
(Ⅱ)当m>0,若函数g(x)=f(x)+1-m有三个零点,求m的取值范围.
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的递增区间即可;
(Ⅱ)求出g(x)的导数,解关于导函数的不等式,求出函数的单调区间,得到函数的极值,结合函数的零点问题得到关于m的不等式组,解出即可.
解答 解:(Ⅰ)f′(x)=3mx2-6mx,
令f′(x)>0,即3mx2-6mx>0,
当m>0时,解得x<0或x>2,则函数f(x)的单调增区间是(-∞,0)和(2,+∞);
当m<0时,解得0<x<2,则函数f(x)的单调增区间是(0,2);
综上,当m<0时,函数f(x)的单调增区间是(-∞,0)和(2,+∞);
当m<0时,函数f(x)的单调增区间是(0,2).
(Ⅱ) 由g(x)=f(x)+1-m及f(x)=mx3-3mx2,
当m>0,g(x)=mx3-3mx2+1-m,g′(x)=3mx(x-2),
当g′(x)>0,解得x<0或x>2,则函数g(x)的单调增区间是(-∞,0)和(2,+∞);
当g′(x)<0,得0<x<2,则函数g(x)的单调减区间是(0,2),
所以g(x)有极大值g(0)=1-m和极小值g(2)=1-5m,
因为g(x)有三个零点,则$\left\{\begin{array}{l}{g(0)=1-m>0}\\{g(2)=1-5m<0}\end{array}\right.$,
得:$\frac{1}{5}$<m<1.
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及分类讨论思想,是一道中档题.

练习册系列答案
相关题目
19.如图,在直角坐标系内,射线OT落在60°的终边上,任作一条射线OA,则射线落在∠xOT内的概率是( )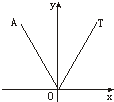

| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | 以上全不对 |
16.曲线y=xex+1在点(1,e+1)处的切线方程是( )
| A. | 2ex-y-e+1=0 | B. | 2ey-x+e+1=0 | C. | 2ex+y-e+1=0 | D. | 2ey+x-e+1=0 |
13.双曲线$\frac{x^2}{5}$-$\frac{{y{\;}^2}}{4}$=1的焦点坐标为( )
| A. | (3,0)和(-3,0) | B. | (2,0)和(-2,0) | C. | (0,3)和(0,-3) | D. | (0,2)和(0,-2) |
