题目内容
如图，在△ABC中，已知AB=10，AC=14，B=| π |
| 3 |
（Ⅰ）求∠ADB的值；
（Ⅱ）求sin∠DAC的值．
考点：余弦定理的应用,正弦定理的应用
专题：解三角形
分析：（Ⅰ）利用余弦定理，即可得出结论；
（Ⅱ）直接利用余弦定理求解即可．
（Ⅱ）直接利用余弦定理求解即可．
解答：
解：（Ⅰ）在△ADC中，由余弦定理可得BC=16，BD=10∴AD=10，
∵cos∠ADC=
=
=-
，…（3分）
∴cos∠ADB=cos（180°-∠ADC）=-cos∠ADC=
，…（5分）
∴∠ADB=60° …（6分）
（Ⅱ）cos∠DAC=
=
=
，…（9分）
可得sin∠DAC=
=
．…（12分）
∵cos∠ADC=
| AD2+DC2-AC2 |
| 2AD•DC |
| 102+62-142 |
| 2×10×6 |
| 1 |
| 2 |
∴cos∠ADB=cos（180°-∠ADC）=-cos∠ADC=
| 1 |
| 2 |
∴∠ADB=60° …（6分）
（Ⅱ）cos∠DAC=
| AD2+AC2-AD2 |
| 2AD•AC |
| 100+196-36 |
| 2×10×14 |
| 13 |
| 14 |
可得sin∠DAC=
| 1-cos2∠DAC |
3
| ||
| 14 |
点评：本题考查余弦定理的应用，基本知识的考查．
练习册系列答案
快乐5加2金卷系列答案
相关题目
设复数z=
，则复数z2的实部与虚部的和为（ ）
| 2i |
| -1+i |
| A、0 | B、2 | C、-2 | D、4 |
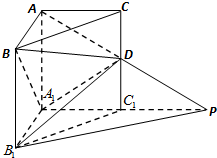如图，在直三棱柱ABC-A1B1C1中，BC=
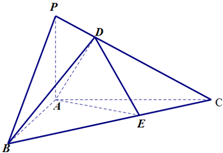如图，在△ABC中，∠BAC=90°，AC=2AB，PA垂直△ABC所在的平面，PC与△ABC所在的平面成30°角，点D在线段PC上，点E在线段BC上．
如图所示，ABCDEF是边长为1的正六边形，现从六个顶点任取三个顶点构成三角形，该三角形的面积S是一随机变量．