题目内容
设f（x）=x2（2-x），则f（x）的单调增区间是（ ）
A、x∈（0，
| ||
B、x∈（
| ||
| C、x∈（-∞，0） | ||
D、x∈（-∞，0）∪（
|
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：先求出函数的导函数，令导函数大于0，解不等式求出即可．
解答：
解：f（x）=x2（2-x），
∴f′（x）=x（4-3x），
令f′（x）＞0，解得：0＜x＜
，
故选：A．
∴f′（x）=x（4-3x），
令f′（x）＞0，解得：0＜x＜
| 4 |
| 3 |
故选：A．
点评：本题考察了函数的单调性，导数的应用，是一道基础题．
练习册系列答案
相关题目
过双曲线
-
=1（a＞0）的右焦点F作一条直线，当直线斜率为2时，直线与双曲线左、右两支各有一个交点；当直线斜率为3时，直线与双曲线右支有两个不同交点，则双曲线离心率的取值范围是 ．
| x2 |
| a2 |
| y2 |
| 5-a2 |
设复数z1=1+i，z2=2+bi，若
为纯虚数，则实数b=（ ）
| z2 |
| z1 |
| A、2 | B、1 | C、-1 | D、-2 |
已知平面向量
=（4，1），
=（x，-2），且2
+
与3
-4
平行，则x=（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、8 | ||
B、-
| ||
| C、-8 | ||
D、
|
若数列{an}的前n项和为Sn=n2+1，则向量
=（a1，a4）的模为（ ）
| m |
| A、53 | ||
| B、50 | ||
C、
| ||
D、5
|
设α表示平面，a、b、l表示直线，给出下列命题，
①
⇒l⊥α；②
⇒b⊥α；③
⇒a⊥α；④直线l与平面α内无数条直线垂直，则l⊥α．
其中正确结论的个数为（ ）
①
|
|
|
其中正确结论的个数为（ ）
| A、0 | B、1 | C、2 | D、3 |
设数列{an}的前n项和为Sn，a1=1，an=
+2（n-1），（n∈N*），若S1+
+
+…+
-（n-1）2=2015，则n的值为（ ）
| Sn |
| n |
| S2 |
| 2 |
| S3 |
| 3 |
| Sn |
| n |
| A、1008 | B、1007 |
| C、2014 | D、2015 |
下列函数中，在区间（0，
）上为增函数的是（ ）
| π |
| 2 |
| A、y=sin2x |
| B、y=cosx |
| C、y=-cos2x |
| D、y=-tanx |
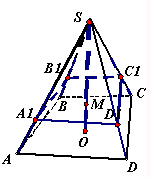如图，在四棱锥S-ABCD中，SO⊥平面ABCD，O为垂足，点M在SO上，且SM：MO=2：1，经过点M作与底面ABCD平行的平面α，分别交棱SA、SB、SC、SD于A1、B1、C1、D1