题目内容
14.$\underset{lim}{n→∞}$$\frac{{C}_{n}^{n-2}+{2C}_{n}^{n}}{(n+2)^{2}}$=$\frac{1}{2}$.分析 先利用组合的性质进行展开,再求极限.
解答 解:$\underset{lim}{n→∞}$$\frac{{C}_{n}^{n-2}+{2C}_{n}^{n}}{(n+2)^{2}}$=$\underset{lim}{n→∞}$$\frac{\frac{n(n-1)}{2}+2}{{n}^{2}+2n+2}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查组合的展开式及求极限的求法,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.设复数z满足$\frac{1+z}{1-z}$=i,则z的虚部为( )
| A. | -i | B. | i | C. | 1 | D. | -1 |
19.若复数z满足z(1-i)=i2017(i是虚数单位),则复数z等于( )
| A. | $\frac{1}{2}$+$\frac{1}{2}$i | B. | -$\frac{1}{2}$-$\frac{1}{2}$i | C. | -$\frac{1}{2}$+$\frac{1}{2}$i | D. | $\frac{1}{2}$-$\frac{1}{2}$i |
6.如果0<a<1<b,c=logab+logba+2( )
| A. | c>0 | B. | c≥0 | C. | c<0 | D. | c≤0 |
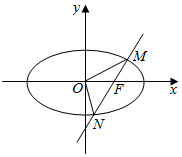 如图:已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),过右焦点F(1,0)的直线l与椭圆E交于M、N两点,且满足$\overrightarrow{MF}$=$\frac{1}{2}$$\overrightarrow{FN}$.
如图:已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),过右焦点F(1,0)的直线l与椭圆E交于M、N两点,且满足$\overrightarrow{MF}$=$\frac{1}{2}$$\overrightarrow{FN}$.