题目内容
5.若实数x,y满足不等式组$\left\{\begin{array}{l}y≥0\\ 2x-y+3≥0\\ x+y-1≤0\end{array}\right.$,则z=2y-|x|的最小值是-$\frac{3}{2}$.分析 作出不等式组对应的平面区域,利用目标函数的几何意义,利用平移法进行判断即可.
解答 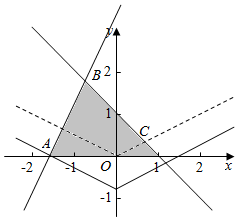 解:作出不等式组对应的平面区域如图
解:作出不等式组对应的平面区域如图
由z=2y-|x|得y=$\frac{1}{2}$|x|+$\frac{1}{2}$z,
平移y=$\frac{1}{2}$|x|+$\frac{1}{2}$z,由图象知当y=$\frac{1}{2}$|x|+$\frac{1}{2}$z经过点A时,$\frac{1}{2}$z最小,此时z最小,
由$\left\{\begin{array}{l}{y=0}\\{2x-y+3=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=-\frac{3}{2}}\\{y=0}\end{array}\right.$,即A(-$\frac{3}{2}$,0),
此时z=-|-$\frac{3}{2}$|=-$\frac{3}{2}$,
故答案为:-$\frac{3}{2}$.
点评 本题主要考查线性规划的应用,利用数形结合是解决本题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
15.某中学数学组来了5名即将毕业的大学生进行教学实习活动,现将他们分配到高一年级的1,2,3三个班实习,每班至少一名,最多两名,则不同的分配方案有( )
| A. | 30种 | B. | 90种 | C. | 150种 | D. | 180种 |
13.($\overrightarrow{AB}$+$\overrightarrow{MB}$)+($\overrightarrow{BO}$+$\overrightarrow{OM}$)+$\overrightarrow{BA}$化简后为( )
| A. | $\overrightarrow{0}$ | B. | $\overrightarrow{AB}$ | C. | $\overrightarrow{BA}$ | D. | $\overrightarrow{OM}$ |
20. 某中学共有1000名学生参加考试,成绩如表:
某中学共有1000名学生参加考试,成绩如表:
(1)为了了解同学们的具体情况,学校将采取分层抽样的方法,抽取100名同学进行问卷调查,甲同学在本次测试中成绩为95分,求他被抽中的概率.
(2)本次数学成绩的优秀成绩为110分,试估计该中学达到优秀线的人数.
(3)作出频率分布直方图,并据此估计该校本次考试的平均分(用同一组中得到数据用该组区间的中点值作代表)
 某中学共有1000名学生参加考试,成绩如表:
某中学共有1000名学生参加考试,成绩如表:| 成绩分组 | [0,30) | [30,60) | [60,90) | [90,120) | [120,150) |
| 人 数 | 60 | 90 | 300 | x | 160 |
(2)本次数学成绩的优秀成绩为110分,试估计该中学达到优秀线的人数.
(3)作出频率分布直方图,并据此估计该校本次考试的平均分(用同一组中得到数据用该组区间的中点值作代表)
