题目内容
6．如果0＜a＜1＜b，c=logab+logba+2（ ）| A． | c＞0 | B． | c≥0 | C． | c＜0 | D． | c≤0 |
分析 利用对数的性质以及基本不等式求解即可．
解答 解：0＜a＜1＜b，logab＜0，logba＜0，
logab+logba=logab+$\frac{1}{lo{g}_{a}b}$=-（-logab-$\frac{1}{lo{g}_{a}b}$）≤-2$\sqrt{-lo{g}_{a}b•（-\frac{1}{lo{g}_{a}b}）}$=-2．
当且仅当logab=-1时取等号，
logab+logba+2的取值范围：（-∞，0]．
故选：D．
点评 本题考查对数的运算性质，基本不等式的应用，考查计算能力．
练习册系列答案
相关题目
3．
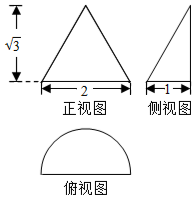已知某几何体的三视图如图所示，则该几何体的表面积为（ ）
已知某几何体的三视图如图所示，则该几何体的表面积为（ ）| A． | $\frac{5π}{2}+\sqrt{3}$ | B． | $\frac{3π}{2}+2$ | C． | $\frac{π}{2}+\sqrt{3}$ | D． | $\frac{3π}{2}+\sqrt{3}$ |
20．
某中学共有1000名学生参加考试，成绩如表：
（1）为了了解同学们的具体情况，学校将采取分层抽样的方法，抽取100名同学进行问卷调查，甲同学在本次测试中成绩为95分，求他被抽中的概率．
（2）本次数学成绩的优秀成绩为110分，试估计该中学达到优秀线的人数．
（3）作出频率分布直方图，并据此估计该校本次考试的平均分（用同一组中得到数据用该组区间的中点值作代表）
某中学共有1000名学生参加考试，成绩如表：| 成绩分组 | [0，30） | [30，60） | [60，90） | [90，120） | [120，150） |
| 人 数 | 60 | 90 | 300 | x | 160 |
（2）本次数学成绩的优秀成绩为110分，试估计该中学达到优秀线的人数．
（3）作出频率分布直方图，并据此估计该校本次考试的平均分（用同一组中得到数据用该组区间的中点值作代表）