题目内容
8.设函数f(x)=($\frac{1}{3}$)x的图象与直线y=5-x交点的横坐标为x1、x2,函数g(x)=log${\;}_{\frac{1}{3}}$x的图象与直线y=5-x交点的横坐标为x3,x4则x1+x2+x3+x4的值为10.分析 x1、x2是( $\frac{1}{3}$)x=5-x的两个根,得到x1=5-$({\frac{1}{3})}^{{x}_{1}}$,x2=5-$({\frac{1}{3})}^{{x}_{2}}$,再根据f(x)与g(x)互为反函数得到x3=y2=$({\frac{1}{3})}^{{x}_{2}}$,x4=y1=$({\frac{1}{3})}^{{x}_{1}}$,问题得以解决.
解答 解:函数f(x)=($\frac{1}{3}$)x的图象与直线y=5-x交点的横为x1、x2,
∴x1、x2是($\frac{1}{3}$)x=5-x的两个根,
∴x1=5-$({\frac{1}{3})}^{{x}_{1}}$,x2=5-$({\frac{1}{3})}^{{x}_{2}}$,
∵f(x)=($\frac{1}{3}$)x的图象与g(x)=log${\;}_{\frac{1}{3}}$x关于y=x对称,
∴x3=y2=$({\frac{1}{3})}^{{x}_{2}}$,x4=y1=$({\frac{1}{3})}^{{x}_{1}}$,
∴x1+x2+x3+x4═5-$({\frac{1}{3})}^{{x}_{1}}$+5-$({\frac{1}{3})}^{{x}_{2}}$+$({\frac{1}{3})}^{{x}_{2}}$+$({\frac{1}{3})}^{{x}_{1}}$=10.
故答案为:10.
点评 本题考查了指数函数和对数函数的性质,以及方程的根的问题,关键是f(x)与g(x)互为反函数,属于中档题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.($\overrightarrow{AB}$+$\overrightarrow{MB}$)+($\overrightarrow{BO}$+$\overrightarrow{OM}$)+$\overrightarrow{BA}$化简后为( )
| A. | $\overrightarrow{0}$ | B. | $\overrightarrow{AB}$ | C. | $\overrightarrow{BA}$ | D. | $\overrightarrow{OM}$ |
3.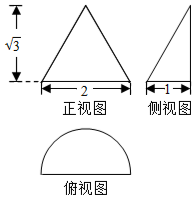 已知某几何体的三视图如图所示,则该几何体的表面积为( )
已知某几何体的三视图如图所示,则该几何体的表面积为( )
 已知某几何体的三视图如图所示,则该几何体的表面积为( )
已知某几何体的三视图如图所示,则该几何体的表面积为( )| A. | $\frac{5π}{2}+\sqrt{3}$ | B. | $\frac{3π}{2}+2$ | C. | $\frac{π}{2}+\sqrt{3}$ | D. | $\frac{3π}{2}+\sqrt{3}$ |
13.复数z满足z(1-3i)=10(i是虚数单位),则复数z等于( )
| A. | -1+3i | B. | 1+3i | C. | -1-3i | D. | 1-3i |
20. 某中学共有1000名学生参加考试,成绩如表:
某中学共有1000名学生参加考试,成绩如表:
(1)为了了解同学们的具体情况,学校将采取分层抽样的方法,抽取100名同学进行问卷调查,甲同学在本次测试中成绩为95分,求他被抽中的概率.
(2)本次数学成绩的优秀成绩为110分,试估计该中学达到优秀线的人数.
(3)作出频率分布直方图,并据此估计该校本次考试的平均分(用同一组中得到数据用该组区间的中点值作代表)
 某中学共有1000名学生参加考试,成绩如表:
某中学共有1000名学生参加考试,成绩如表:| 成绩分组 | [0,30) | [30,60) | [60,90) | [90,120) | [120,150) |
| 人 数 | 60 | 90 | 300 | x | 160 |
(2)本次数学成绩的优秀成绩为110分,试估计该中学达到优秀线的人数.
(3)作出频率分布直方图,并据此估计该校本次考试的平均分(用同一组中得到数据用该组区间的中点值作代表)
17.现从男、女共8名学生干部中选出3名同学(要求3人中既有男同学又有女同学)分别参加全校“资源”、“生态”和“环保”三个夏令营活动,共有270种不同的安排,那么8名学生中男、女同学的人数分别是( )
| A. | 男同学1人,女同学7人 | B. | 男同学2人,女同学6人 | ||
| C. | 男同学3人,女同学5人 | D. | 男同学4人,女同学4人 |
18.设集合A={x|2x-1>5},集合B={x|y=lg(6-x)},则A∩B等于( )
| A. | (3,6) | B. | [3,6] | C. | (3,6] | D. | [3,6) |