题目内容
4．设复数z满足$\frac{1+z}{1-z}$=i，则z的虚部为（ ）| A． | -i | B． | i | C． | 1 | D． | -1 |
分析 把已知的等式变形，然后利用复数代数形式的乘除运算化简求得z，则答案可求．
解答 解：由$\frac{1+z}{1-z}$=i，得1+z=i-iz，
即（1+i）z=-1+i，
∴$z=\frac{-1+i}{1+i}=\frac{（-1+i）（1-i）}{（1+i）（1-i）}=\frac{2i}{2}=i$，
∴z的虚部为1．
故选：C．
点评 本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础题．
练习册系列答案
相关题目
15．某中学数学组来了5名即将毕业的大学生进行教学实习活动，现将他们分配到高一年级的1，2，3三个班实习，每班至少一名，最多两名，则不同的分配方案有（ ）
| A． | 30种 | B． | 90种 | C． | 150种 | D． | 180种 |
9．
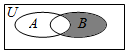若全集U=R，A={0，1，2，3}，B={2，3，4，5}，则Venn图中阴影部分表示的集合为（ ）
若全集U=R，A={0，1，2，3}，B={2，3，4，5}，则Venn图中阴影部分表示的集合为（ ）| A． | {0，1} | B． | {2，3} | C． | {4，5} | D． | {0，1，4，5} |
13．（$\overrightarrow{AB}$+$\overrightarrow{MB}$）+（$\overrightarrow{BO}$+$\overrightarrow{OM}$）+$\overrightarrow{BA}$化简后为（ ）
| A． | $\overrightarrow{0}$ | B． | $\overrightarrow{AB}$ | C． | $\overrightarrow{BA}$ | D． | $\overrightarrow{OM}$ |