题目内容
18.已知函数f(x)=$\frac{1}{3}$x3+ax2-bx (a,b∈R).若y=f(x)图象上的点(1,-$\frac{11}{3}$)处的切线斜率为-4.(1)求a、b的值;
(2)求y=f(x)的极大值;
(3)对?x∈[-2,3],都有f(x)-k<0,求k的取值范围.
分析 (1)求出函数的导数,得到关于a,b的方程组,解出即可;
(2)求出f(x)的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最大值即可;
(3)根据函数的单调性求出函数的最大值,从而求出k的范围即可.
解答 解:(1)∵f′(x)=x2+2ax-b,
∴由题意可知:f′(1)=-4且f(1)=-$\frac{11}{3}$.
即$\left\{\begin{array}{l}{1+2a-b=-4}\\{\frac{1}{3}+a-b=-\frac{11}{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=3}\end{array}\right.$;
(2)由(1)知:f(x)=$\frac{1}{3}$x3-x2-3x,
f′(x)=x2-2x-3=(x+1)(x-3)
令f′(x)=0,得x1=-1,x2=3.
由此可知,当x变化时,f′(x),f(x)的变化情况如下表:
| x | (-∞,-1) | -1 | (-1,3) | 3 | (3,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
(3)由(2)知y=f(x)在(-2,-1)内是增函数,在(-1,3)内是减函数,所以函数的最大值为$\frac{5}{3}$,
∵对?x∈[-2,3],都有f(x)-k<0.
∴k>$\frac{5}{3}$,∴k的取值范围为($\frac{5}{3}$,+∞).
点评 本题考查了函数的单调性、最值、极值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
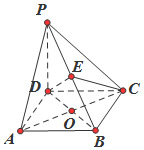 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=2$\sqrt{3}$,且AC,BD交于点O,E是PB上任意一点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=2$\sqrt{3}$,且AC,BD交于点O,E是PB上任意一点.