题目内容
10．过点M（0，4）的直线l交抛物线x2=4y于AA，B两点，若△AOM与△BOM的面积比为2：1（O为坐标原点），则直线l的斜率为±$\frac{\sqrt{2}}{2}$．分析 直线l方程为y=kx+4，代入椭圆方程，由韦达定理，三角形的面积公式，即可求得A和B点坐标，代入求得求得直线的斜率．
解答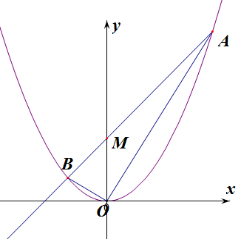 
解：设直线l方程为y=kx+4，A（x1，y1），B（x2，y2），
由$\left\{\begin{array}{l}{y=kx+4}\\{{x}^{2}=4y}\end{array}\right.$，整理得：x2-4kx-16=0，
由韦达定理可知：x1+x2=4k，x1•x2=-16，
△AOM与△BOM的面积比为2：1，
∴丨x1丨=2丨x2丨，则x1=-2x2，
∴$\left\{\begin{array}{l}{{x}_{1}=-4\sqrt{2}}\\{{x}_{2}=2\sqrt{2}}\end{array}\right.$，$\left\{\begin{array}{l}{{x}_{1}=4\sqrt{2}}\\{{x}_{2}=-2\sqrt{2}}\end{array}\right.$，
k=±$\frac{\sqrt{2}}{2}$，
直线l的斜率$\frac{\sqrt{2}}{2}$，
故答案为：$\frac{\sqrt{2}}{2}$．
点评 本题考查直线与抛物线的位置关系，韦达定理，三角形的面积公式，考查计算能力，属于中档题．
练习册系列答案
相关题目
20．已知直线m、n与平面α、β，则下列说法正确的是（ ）
| A． | 若m∥α，n∥α，则m∥n | B． | 若m∥α，n⊥α，则n⊥m | C． | 若m⊥α，n⊥β，则α⊥β | D． | 若m⊥α，n⊥β，则n⊥m |