题目内容
4.给出下列命题:(1)“若x>2,则x>3”的否命题;
(2)“?a∈(0,+∞),函数y=ax在定义域内单调递增”的否定;
(3)“π是函数y=sinx的一个周期”或“2π是函数y=sin2x的一个周期”;
(4)“x2+y2=0”是“xy=0”的必要条件;
其中真命题的序号是(1)(2)(3).
分析 由命题的否命题,即可判断(1);可举a=1,则为常数函数,即可判断(2);
运用正弦函数的周期公式,即可判断(3);运用充分必要条件的定义,即可判断(4).
解答 解:对于(1),“若x>2,则x>3”的否命题为“若x≤2,则x≤3”,为真命题;
对于(2),若a=1,则y=1为常数函数,则命题“?a∈(0,+∞),函数y=ax在定义域内单调递增”
为假命题,故其否定为真命题;
对于(3),y=sinx的最小正周期为2π,y=sin2x的最小正周期为π,
则命题“π是函数y=sinx的一个周期”或“2π是函数y=sin2x的一个周期”为真命题;
对于(3),“x2+y2=0”可推出“xy=0”,反之,不一定推出,故为充分条件,则为假命题.
则真命题的序号是(1)(2)(3).
故答案为:(1)(2)(3)
点评 本题考查简易逻辑的有关知识,考查命题的否定和否命题的区别,考查充分必要条件和三角函数的周期的求法,考查判断能力,属于基础题和易错题.

练习册系列答案
相关题目
15.已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=3x-1-m(m为常数),则f(log3$\frac{1}{5}$)=( )
| A. | 4 | B. | -4 | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
12.已知数列{an}的首项a1=2,数列{bn}为等比数列,且${b_n}=\frac{{{a_{n+1}}}}{a_n}$,若b10b11=2,则a21=( )
| A. | 29 | B. | 210 | C. | 211 | D. | 212 |
9.已知函数y=f(x)是定义在上的奇函数,且当x>0时,f(x)=2x-1-3,则f(f(1))=( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
13.已知直线x=$\frac{π}{4}$和x=$\frac{5π}{4}$是函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)图象的两条相邻的对称轴,则φ=( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
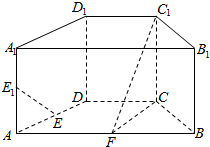 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、E1、F分别是棱AD、AA1、AB的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、E1、F分别是棱AD、AA1、AB的中点.