题目内容
14.设复数z=x+(y-1)i(x,y∈R),若|z|≤1,则y≤x的概率为$\frac{1}{4}-\frac{1}{2π}$.分析 由题意易得所求概率为弓形的面积与圆的面积之比,分别求面积可得.
解答 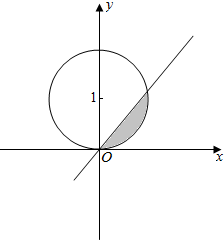 解:∵复数z=x+(y-1)i(x,y∈R)且|z|≤1,
解:∵复数z=x+(y-1)i(x,y∈R)且|z|≤1,
∴|z|=$\sqrt{{x}^{2}+(y-1)^{2}}$≤1,即x2+(y-1)2 ≤1,
∴点(x,y)在(0,1)为圆心1为半径的圆及其内部,
而y≤x表示直线y=x左上方的部分,(图中阴影弓形)
∴所求概率为弓形的面积与圆的面积一般的之比,
∴所求概率P=$\frac{π•{1}^{2}-\frac{3}{4}π•{1}^{2}-\frac{1}{2}×1×1}{π•{1}^{2}}$=$\frac{1}{4}-\frac{1}{2π}$
故答案为:$\frac{1}{4}-\frac{1}{2π}$.
点评 本题考查几何概型,涉及复数以及圆的知识,属基础题.

练习册系列答案
相关题目
4.设命题p:?x0∈(0,+∞),e${\;}^{{x}_{0}}$+x0=5.命题q:?x∈(0,+∞),$\frac{3}{x+1}$+x≥2$\sqrt{3}$-1.那么,下列命题为真命题的是( )
| A. | ¬q | B. | (¬p)∨(¬q) | C. | p∧q | D. | p∧(¬q) |
2.函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-2,x≤1}\\{-lo{g}_{2}(x+1),x>1}\end{array}\right.$且f(a)=-3,则f(5-a)=( )
| A. | -$\frac{7}{4}$ | B. | -$\frac{5}{4}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{1}{4}$ |
9.圆心在直线x+y=0上且过两x2+y2-2x=0,x2+y2+2y=0的交点的圆的方程为( )
| A. | x2+y2-x+y-$\frac{1}{2}$=0 | B. | x2+y2+x-y-$\frac{1}{2}$=0 | C. | x2+y2-x+y=0 | D. | x2+y2+x-y=0 |
6.函数$f(x)={log_x}(6{x^2}-7x+2)$的定义域是( )
| A. | $(0{,_{\;}}\frac{1}{2})∪(\frac{2}{3}{,_{\;}}1)∪(1{,_{\;}}+∞)$ | B. | $(-∞{,_{\;}}\frac{1}{2})∪(\frac{2}{3}{,_{\;}}+∞)$ | ||
| C. | $(\frac{1}{2}{,_{\;}}\frac{2}{3})$ | D. | $(0{,_{\;}}\frac{1}{2})∪(\frac{2}{3}{,_{\;}}1)∪(1{,_{\;}}\frac{3}{2})$ |
3.奇函数f(x)在(0,+∞)上递增,且f(-2)=0,则不等式 $\frac{f(x)-f(-x)}{x}$<0的解集为( )
| A. | (-∞,-2)∪(0,2) | B. | (-2,0)∪(0,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-2,0)∪(2,+∞) |