题目内容
7.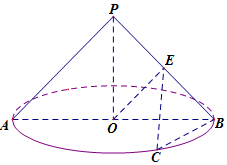 如图,圆锥的顶点为P,底面圆O半径为1,圆锥侧面积为$\sqrt{2}π$,AB是圆O的直径,点C是圆O上的点,且$BC=\sqrt{2}$.
如图,圆锥的顶点为P,底面圆O半径为1,圆锥侧面积为$\sqrt{2}π$,AB是圆O的直径,点C是圆O上的点,且$BC=\sqrt{2}$.(Ⅰ)求异面直线PA与BC所成角;
(Ⅱ)点E在线段PB上,求CE+OE的最小值.
分析 (Ⅰ)延长CO交圆O于D,连AD,∠PAD是异面直线PA与BC所成角,即可求异面直线PA与BC所成角;
(Ⅱ)当E为PB中点时,CE+OE最小,即可求CE+OE的最小值.
解答 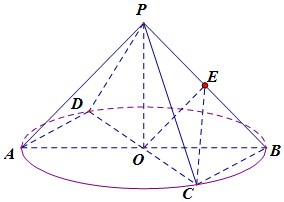 解:(Ⅰ)由${S_侧}=πrl=\sqrt{2}π,r=1$,得$l=PA=\sqrt{2},PO=1$.
解:(Ⅰ)由${S_侧}=πrl=\sqrt{2}π,r=1$,得$l=PA=\sqrt{2},PO=1$.
延长CO交圆O于D,连AD,由△OBC≌△ODA,得∠ADO=∠BCO,得AD∥BC,所以∠PAD是异面直线PA与BC所成角.
因为$PA=AD=PD=\sqrt{2}$,所以∠PAD=60°.
(Ⅱ)当E为PB中点时,由OB=OP=1,得$OE⊥PB,OE=\frac{{\sqrt{2}}}{2}$,
由$CP=CB=\sqrt{2}$,得$CE⊥PB,CE=\frac{{\sqrt{6}}}{2}$,
所以当E为PB中点时,CE+OE最小,最小值为$\frac{{\sqrt{6}+\sqrt{2}}}{2}$.
点评 本题考查线线角,考查空间距离的计算,属于中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
17.已知数列{an}是等差数列,且a2+a3+a10+a11=48,则a5+a8等于( )
| A. | 12 | B. | 18 | C. | 24 | D. | 30 |
2.一条直线与两条异面直线中的一条平行,则它和另一条的位置关系是( )
| A. | 异面 | B. | 相交 | C. | 异面或平行 | D. | 相交或异面 |
19.一个几何体的三视图如图,则该几何体的体积为( )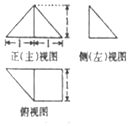

| A. | 2 | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
17.已知底面边长为$2\sqrt{3}$的正三棱锥O-ABC的体积为$\sqrt{3}$,且A,B,C在球O上,则球的体积是( )
| A. | $\frac{{20\sqrt{5}π}}{3}$ | B. | 8π | C. | 20π | D. | $4\sqrt{3}π$ |
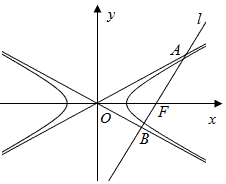 如图所示,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,过F的直线l交双曲线的渐近线于A,B两点,且直线l的倾斜角是渐近线OA倾斜角的2倍,若$\overrightarrow{AF}=2\overrightarrow{FB}$,则该双曲线的离心率为$\frac{2\sqrt{3}}{3}$.
如图所示,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,过F的直线l交双曲线的渐近线于A,B两点,且直线l的倾斜角是渐近线OA倾斜角的2倍,若$\overrightarrow{AF}=2\overrightarrow{FB}$,则该双曲线的离心率为$\frac{2\sqrt{3}}{3}$.