题目内容
18.已知函数f(x)=$\frac{1}{x}$+alnx(a∈R,且a≠0).(1)若函数f(x)在区间(2016,+∞)上单调递增,求实数a的取值范围;
(2)若在区间[1,e]上至少存在一点x0.使得f(x0)<0成立,求实数a的取值范围.
分析 (1)求出函数的导数,通过讨论a的范围,解关于导函数的不等式,求出a的范围即可;
(2)若在区间(0,e]上存在一点x0,使得f(x0)<0成立,其充要条件是f(x)在区间(0,e]上的最小值小于0即可.利用导数研究函数在闭区间[1,e]上的最小值,先求出导函数f'(x),然后讨论研究函数在[1,e]上的单调性,将f(x)的各极值与其端点的函数值比较,其中最小的一个就是最小值.
解答 解:(1)f′(x)=$\frac{ax-1}{{x}^{2}}$,且a≠0,(x>0),
若a<0,f′(x)<0在(0,+∞)恒成立,不合题意,
若a>0,令f′(x)>0,解得:x>$\frac{1}{a}$,
故f(x)在($\frac{1}{a}$,+∞)递增,
若函数f(x)在区间(2016,+∞)上单调递增,
则$\frac{1}{a}$<2016,解得:a>$\frac{1}{2016}$;
(2)因为f′(x)=$\frac{ax-1}{{x}^{2}}$,且a≠0,
令f'(x)=0,得到x=$\frac{1}{a}$,
若在区间[1,e]上存在一点x0,使得f(x0)<0成立,
其充要条件是f(x)在区间[1,e]上的最小值小于0即可.
①当a<0时,f'(x)<0对x∈(0,+∞)成立,
所以,f(x)在区间[1,e]上单调递减,
故f(x)在区间[1,e]上的最小值为f(e)=$\frac{1}{e}$+alne=$\frac{1}{e}$+a,
由$\frac{1}{e}$+a<0,得a<-$\frac{1}{e}$,即a∈(-∞,-$\frac{1}{e}$);
②当a>0时,
若e≤$\frac{1}{a}$,则f'(x)≤0对x∈[1,e]成立,
所以f(x)在区间[1,e]上单调递减,
所以,f(x)在区间[1,e]上的最小值为f(e)=$\frac{1}{e}$+alne=$\frac{1}{e}$+a>0,
显然,f(x)在区间[1,e]上的最小值小于0不成立;
若1<$\frac{1}{a}$<e,即1>a>$\frac{1}{e}$时,则有
| x | (1,$\frac{1}{a}$) | $\frac{1}{a}$ | ($\frac{1}{a}$,e) |
| f'(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
由f($\frac{1}{a}$)=a+aln$\frac{1}{a}$=a(1-lna)<0,
得1-lna<0,解得a>e,即a∈(e,+∞)舍去;
当0<$\frac{1}{a}$<1,即a>1,即有f(x)在[1,e]递增,
可得f(1)取得最小值,且为1,f(1)>0,不成立.
综上,由①②可知a<-$\frac{1}{e}$符合题意.
点评 本题考查利用导函数来研究函数的极值以及在闭区间上的最值问题.在利用导函数来研究函数的极值时,分三步①求导函数,②求导函数为0的根,③判断根左右两侧的符号,若左正右负,原函数取极大值;若左负右正,原函数取极小值,体现了转化的思想和分类讨论的思想,同时考查学生的计算能力.

| A. | $\frac{{2\sqrt{2}}}{3}$ | B. | $\frac{{\sqrt{7}}}{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
| A. | 0 | B. | -1 | C. | -2 | D. | -3 |
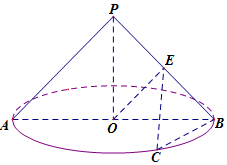 如图,圆锥的顶点为P,底面圆O半径为1,圆锥侧面积为$\sqrt{2}π$,AB是圆O的直径,点C是圆O上的点,且$BC=\sqrt{2}$.
如图,圆锥的顶点为P,底面圆O半径为1,圆锥侧面积为$\sqrt{2}π$,AB是圆O的直径,点C是圆O上的点,且$BC=\sqrt{2}$.