题目内容
15．△ABC中，已知角A，B，C所对的边分别为a，b，c，$\frac{cosA}{a}$+$\frac{cosC}{c}$=$\frac{1}{b}$，b=4，且a＞c．（1）求ac的值；
（2）若△ABC的面积为2$\sqrt{7}$，求a，c的值．
分析 （1）运用余弦定理，化简整理，计算即可得到ac的值；
（2）由三角形的面积公式可得sinB，求得cosB，再由余弦定理可得a，c关系式，解方程可得a，c的值．
解答 解：（1）$\frac{cosA}{a}$+$\frac{cosC}{c}$=$\frac{1}{b}$，b=4，
可得acosC+ccosA=$\frac{ac}{4}$，
由余弦定理可得a•$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$+c•$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{ac}{4}$，
即有b=$\frac{ac}{4}$，则ac=16；
（2）△ABC的面积为2$\sqrt{7}$，
可得$\frac{1}{2}$acsinB=2$\sqrt{7}$，
即有sinB=$\frac{\sqrt{7}}{4}$，
cosB=±$\sqrt{1-\frac{7}{16}}$=±$\frac{3}{4}$，
b2=a2+c2-2accosB，
即为16=a2+c2-24，或16=a2+c2+24（舍去），
又ac=16，（a＞c＞0），
解得a=4$\sqrt{2}$，c=2$\sqrt{2}$．
点评 本题考查三角形的余弦定理和面积公式的运用，考查化简整理的圆能力，属于中档题．
练习册系列答案
相关题目
5．条件p：|x+1|＞2，条件q：x＞2，则￢p是￢q的（ ）
| A． | 充分非必要条件 | B． | 必要不充分条 | ||
| C． | 充要条件 | D． | 既不充分也不必要的条件 |
6．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的一条渐近线的斜率是$\sqrt{3}$，则此双曲线的离心率等于（ ）
| A． | $\frac{{2\sqrt{2}}}{3}$ | B． | $\frac{{\sqrt{7}}}{2}$ | C． | 2 | D． | $2\sqrt{2}$ |
20．已知 f（sinx）=x，且 $x∈（{0，\frac{π}{2}}）$，则$f（\frac{1}{2}）$ 的值等于（ ）
| A． | $sin\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | $-\frac{π}{6}$ | D． | $\frac{π}{6}$ |
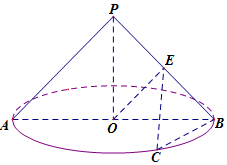如图，圆锥的顶点为P，底面圆O半径为1，圆锥侧面积为$\sqrt{2}π$，AB是圆O的直径，点C是圆O上的点，且$BC=\sqrt{2}$．