题目内容
16.在等差数列{an}中,a1=1,a3+a5=3,若a1,a7,an成等比数列,则n=19.分析 由等差数列通项公式求出公差d=$\frac{1}{6}$,由此根据a1,a7,an成等比数列,能求出n的值.
解答 解:∵在等差数列{an}中,a1=1,a3+a5=3,
∴$\left\{\begin{array}{l}{{a}_{1}=1}\\{{a}_{1}+2d+{a}_{1}+4d=3}\end{array}\right.$,
解得d=$\frac{1}{6}$,
∴${a}_{n}=1+(n-1)×\frac{1}{6}$=$\frac{n}{6}+\frac{5}{6}$,
∵a1,a7,an成等比数列,
∴${{a}_{7}}^{2}={a}_{1}{a}_{n}$,即($\frac{7}{6}+\frac{5}{6}$)2=1×($\frac{n}{6}+\frac{5}{6}$),
解得n=19.
故答案为:19.
点评 本题考查数列的项数n的求法,是基础题,解题时要认真审题,注意等差数列、等比数列的性质的合理运用.

练习册系列答案
相关题目
6.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的一条渐近线的斜率是$\sqrt{3}$,则此双曲线的离心率等于( )
| A. | $\frac{{2\sqrt{2}}}{3}$ | B. | $\frac{{\sqrt{7}}}{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
11.若函数f(x)=sinωx+$\sqrt{3}$cos(ωx+$\frac{π}{3}$)(ω>0)的最小正周期为π,则f(x)在[0,$\frac{π}{4}$]上的最大值为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
8.已知存在实数a,使得关于x的不等式$\sqrt{2x}-a≥\sqrt{9-5x}$恒成立,则a的最大值为( )
| A. | 0 | B. | -1 | C. | -2 | D. | -3 |
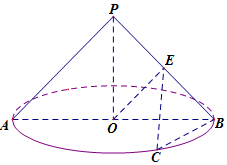 如图,圆锥的顶点为P,底面圆O半径为1,圆锥侧面积为$\sqrt{2}π$,AB是圆O的直径,点C是圆O上的点,且$BC=\sqrt{2}$.
如图,圆锥的顶点为P,底面圆O半径为1,圆锥侧面积为$\sqrt{2}π$,AB是圆O的直径,点C是圆O上的点,且$BC=\sqrt{2}$.