题目内容
17.已知底面边长为$2\sqrt{3}$的正三棱锥O-ABC的体积为$\sqrt{3}$,且A,B,C在球O上,则球的体积是( )| A. | $\frac{{20\sqrt{5}π}}{3}$ | B. | 8π | C. | 20π | D. | $4\sqrt{3}π$ |
分析 正三棱锥的顶点正好是球心,底面为一个小圆,求出小圆半径、三棱锥的高,可得球的半径,即可求出球的体积.
解答 解:正三棱锥的顶点正好是球心,底面为一个小圆,因正△ABC的边长为$2\sqrt{3}$,所以小圆半径r=2,
又因${V_{O-ABC}}=\sqrt{3}$,所以三棱锥的高h=1,
设球半径为R,则$R=\sqrt{{r^2}+{h^2}}=\sqrt{5}$,${V_球}=\frac{4}{3}π{R^3}=\frac{4}{3}π×{(\sqrt{5})^3}=\frac{{20\sqrt{5}π}}{3}$,
故选A.
点评 本题考查球的体积,考查学生的计算能力,求出球的半径是关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
8.已知存在实数a,使得关于x的不等式$\sqrt{2x}-a≥\sqrt{9-5x}$恒成立,则a的最大值为( )
| A. | 0 | B. | -1 | C. | -2 | D. | -3 |
12.已知向量$\overrightarrow{AB}=({x,1}),({x>0}),\overrightarrow{AC}=({1,2}),|{\overrightarrow{BC}}|=\sqrt{5}$,则$\overrightarrow{AB},\overrightarrow{AC}$的夹角为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
9.若角α的终边经过点(-4,3),则tanα=( )
| A. | $\frac{4}{3}$ | B. | $-\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $-\frac{3}{4}$ |
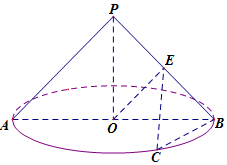 如图,圆锥的顶点为P,底面圆O半径为1,圆锥侧面积为$\sqrt{2}π$,AB是圆O的直径,点C是圆O上的点,且$BC=\sqrt{2}$.
如图,圆锥的顶点为P,底面圆O半径为1,圆锥侧面积为$\sqrt{2}π$,AB是圆O的直径,点C是圆O上的点,且$BC=\sqrt{2}$.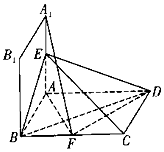 如图,边长为2的正方形A1ABB1所在平面与矩形ABCD所在平面相互垂直,且$AB=\frac{1}{2}BC$,E,F分别是AA1和BC的中点.
如图,边长为2的正方形A1ABB1所在平面与矩形ABCD所在平面相互垂直,且$AB=\frac{1}{2}BC$,E,F分别是AA1和BC的中点.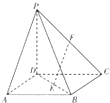 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PD⊥平面ABCD,AD⊥BD,AD=BD=2,E为BD的中点,F为PC的中点.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PD⊥平面ABCD,AD⊥BD,AD=BD=2,E为BD的中点,F为PC的中点.