题目内容
16.已知圆C的方程:x2+y2-2x-4y+m=0.(1)若圆C与直线l:x+2y-4=0相交于M,N两点,且|MN|=$\frac{4\sqrt{5}}{5}$,求m的值;
(2)在(1)条件下,是否存在直线l:x-2y+c=0,使得圆上有四点到直线l的距离为$\frac{\sqrt{5}}{5}$,若存在,求出c的范围,若不存在,说明理由.
分析 (1)化圆的一般式方程为标准式,由已知结合垂径定理求得m值;
(2)把圆上有四点到直线l的距离为$\frac{\sqrt{5}}{5}$,转化为圆心到直线的距离d<1-$\frac{1}{\sqrt{5}}$,求解绝对值的不等式得答案.
解答 解:(1)圆的方程化为(x-1)2+(y-2)2=5-m,
圆心坐标为(1,2),半径为r=$\sqrt{5-m}$,
则圆心C(1,2)到直线l:x+2y-4=0的距离为d=$\frac{|1+2×2-4|}{\sqrt{{1}^{2}+{2}^{2}}}=\frac{1}{\sqrt{5}}$,
由于|MN|=$\frac{4}{\sqrt{5}}$,则$\frac{1}{2}|MN|$=$\frac{2}{\sqrt{5}}$,有${r}^{2}={d}^{2}+(\frac{1}{2}|MN|)^{2}$,
∴5-m=$(\frac{1}{\sqrt{5}})^{2}+(\frac{2}{\sqrt{5}})^{2}$,解得m=4;
(2)假设存在直线l:x-2y+c=0,使得圆上有四点到直线l的距离为$\frac{\sqrt{5}}{5}$,
由于圆心C(1,2),半径r=1,则圆心C(1,2)到直线l:x-2y+c=0的距离为:
d=$\frac{|1-2×2+c|}{\sqrt{{1}^{2}+{2}^{2}}}=\frac{|c-3|}{\sqrt{5}}<|1-\frac{1}{\sqrt{5}}|$,
解得:$2+\frac{\sqrt{5}}{5}<c<4-\frac{\sqrt{5}}{5}$.
点评 本题考查直线与圆的位置关系,考查了点到直线距离公式的应用,考查绝对值不等式的解法,是中档题.

练习册系列答案
相关题目
7.若x,y满足不等式组$\left\{\begin{array}{l}{2x-3y-6≥0}\\{x+y-3≥0}\\{x≤a}\end{array}\right.$,z=x-y的最大值为4,则实数a=( )
| A. | 4 | B. | $\frac{7}{2}$ | C. | 5 | D. | $\frac{9}{2}$ |
11.已知圆(x-2)2+(y+1)2=16的一条直径恰好经过直线x-2y-3=0被圆所截弦的中点,则该直径所在直线的方程为( )
| A. | x-2y=0 | B. | 2x+y-5=0 | C. | 2x+y-3=0 | D. | x-2y+4=0 |
1.圆(x+1)2+(y+2)2=4与圆(x-2)2+(y-2)2=9的公切线有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
6.在平行四边形ABCD中,$\overrightarrow{AC}$•$\overrightarrow{CB}$=0,AC=$\sqrt{2}$,BC=1,若将其沿AC折成直二面角D-AC-B,则AC与BD所成的角的余弦值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
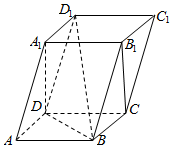 在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧面BCC1B1⊥底面ABCD,B1C=CD=2,BB1=2$\sqrt{2}$.
在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧面BCC1B1⊥底面ABCD,B1C=CD=2,BB1=2$\sqrt{2}$.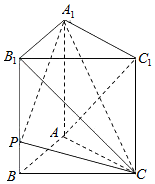 如图,已知直三棱柱ABC-A1B1C1中,AB⊥AC,AB=3,AC=4,B1C⊥AC1.
如图,已知直三棱柱ABC-A1B1C1中,AB⊥AC,AB=3,AC=4,B1C⊥AC1.