题目内容
7.若x,y满足不等式组$\left\{\begin{array}{l}{2x-3y-6≥0}\\{x+y-3≥0}\\{x≤a}\end{array}\right.$,z=x-y的最大值为4,则实数a=( )| A. | 4 | B. | $\frac{7}{2}$ | C. | 5 | D. | $\frac{9}{2}$ |
分析 作出可行域,变形目标函数,平移直线可得z的最值,可得a的方程,解方程可得.
解答  解:作出不等式组$\left\{\begin{array}{l}{2x-3y-6≥0}\\{x+y-3≥0}\\{x≤a}\end{array}\right.$所对应可行域(如图△ABC),
解:作出不等式组$\left\{\begin{array}{l}{2x-3y-6≥0}\\{x+y-3≥0}\\{x≤a}\end{array}\right.$所对应可行域(如图△ABC),
变形目标函数z=x-y可得y=x-z,平移直线y=x可知:
当直线经过点A(a,3-a)时,直线截距最小值,z取最大值,
代值可得a-(3-a)=4,解得a=$\frac{7}{2}$,
故选:B.
点评 本题考查简单线性规划,准确作图是解决问题的关键,属中档题.

练习册系列答案
相关题目
18.微信是腾讯公司推出的一种手机通讯软件,它支持发送语音短信、视频、图片和文字,经推出便风靡全国,甚至涌现出一批在微信的朋友圈销售商的人(简称微商),为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各50名,其中每天玩微信超过4小时的用户为“微信控”,否则称其为“非微信控”,调查结果如下:
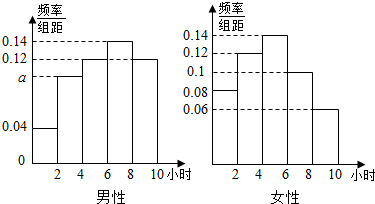
(1)根据以上数据,能否有60%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份,求所抽取5人中“微信控”与“非微信控”的人数;
(3)从(2)中抽取的5人中在随机抽取2人赠送200元的护肤品套装,求这2人至少有1人为“非微信控”的概率.
参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
参数数据:

(1)根据以上数据,能否有60%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份,求所抽取5人中“微信控”与“非微信控”的人数;
(3)从(2)中抽取的5人中在随机抽取2人赠送200元的护肤品套装,求这2人至少有1人为“非微信控”的概率.
参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
参数数据:
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |
15.2015年山东省东部地区土豆种植形成初步规模,出口商在各地设置了大量的代收点.已知土豆收购按质量标准可分为四个等级,某代收点对等级的统计结果如下表所示:
现从该代售点随机抽取了n袋土豆,其中二级品为恰有40袋.
(Ⅰ)求m、n的值;
(Ⅱ)利用分层抽样的方法从这n袋土豆中抽取10袋,剔除特级品后,再从剩余土豆中任意抽取两袋,求抽取的两袋都是一等品的概率.
| 等级 | 特级 | 一级 | 二级 | 三级 |
| 频率 | 0.30 | 2m | m | 0.10 |
(Ⅰ)求m、n的值;
(Ⅱ)利用分层抽样的方法从这n袋土豆中抽取10袋,剔除特级品后,再从剩余土豆中任意抽取两袋,求抽取的两袋都是一等品的概率.
2.已知函数y=f(x)是R上的偶函数,设a=ln$\frac{1}{π}$,b=(lnπ)2,c=ln$\sqrt{π}$,当任意x1、x2∈(0,+∞)时,都有(x1-x2)•[f(x1)-f(x2)]<0,则( )
| A. | f(a)>f(b)>f(c) | B. | f(b)>f(a)>f(c) | C. | f(c)>f(b)>f(a) | D. | f(c)>f(a)>f(b) |
19.阅读如图所示的程序框图,运行相应的程序,则输出的n的值为( )
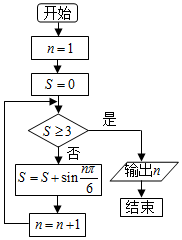

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
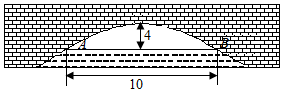 如图,一抛物线型拱桥的拱顶O离水面高4米,水面宽度AB=10米.现有一竹排运送一只货箱欲从桥下经过,已知货箱长20米,宽6米,高2.58米(竹排与水面持平),问货箱能否顺利通过该桥?
如图,一抛物线型拱桥的拱顶O离水面高4米,水面宽度AB=10米.现有一竹排运送一只货箱欲从桥下经过,已知货箱长20米,宽6米,高2.58米(竹排与水面持平),问货箱能否顺利通过该桥?