题目内容
6.正方体ABCD-A1B1C1D1中.(1)求证:BD1⊥平面AB1C;
(2)求AB与平面AB1C所成的角.
分析 (1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能证明BD1⊥平面AB1C.
(2)求出$\overrightarrow{AB}$和平面AB1C的法向量,利用向量法能求出AB与平面AB1C所成的角.
解答 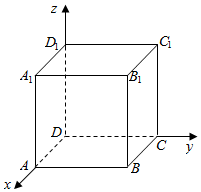 证明:(1)设正方体ABCD-A1B1C1D1中棱长为1,
证明:(1)设正方体ABCD-A1B1C1D1中棱长为1,
以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
B(1,1,0),D1(0,0,1),A(1,0,0),B1(1,1,1),C(0,1,0),
$\overrightarrow{B{D}_{1}}$=(-1,-1,1),$\overrightarrow{A{B}_{1}}$=(0,1,1),$\overrightarrow{AC}$=(-1,1,0),
$\overrightarrow{B{D}_{1}}$•$\overrightarrow{A{B}_{1}}$=0-1+1=0,$\overrightarrow{B{D}_{1}}$•$\overrightarrow{AC}$=1-1+0=0,
∴BD1⊥AB1,BD1⊥AC,
又AB1∩AC=A,∴BD1⊥平面AB1C.
解:(2)$\overrightarrow{AB}$=(0,1,0),
设平面AB1C的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{A{B}_{1}}=y+z=0}\\{\overrightarrow{n}•\overrightarrow{AC}=-x+y=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,1,-1),
设AB与平面AB1C所成的角为θ,
则sinθ=$\frac{|\overrightarrow{AB}•\overrightarrow{n}|}{|\overrightarrow{AB}|•|\overrightarrow{n}|}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$.
∴θ=arcsin$\frac{\sqrt{3}}{3}$.
∴AB与平面AB1C所成的角为arcsin$\frac{\sqrt{3}}{3}$.
点评 本题考查线面垂直的证明,考查线面角的大小的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案| A. | (-∞,5) | B. | -4 | C. | -4或20 | D. | -11 |
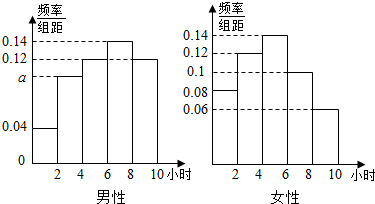
(1)根据以上数据,能否有60%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份,求所抽取5人中“微信控”与“非微信控”的人数;
(3)从(2)中抽取的5人中在随机抽取2人赠送200元的护肤品套装,求这2人至少有1人为“非微信控”的概率.
参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
参数数据:
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |
| 等级 | 特级 | 一级 | 二级 | 三级 |
| 频率 | 0.30 | 2m | m | 0.10 |
(Ⅰ)求m、n的值;
(Ⅱ)利用分层抽样的方法从这n袋土豆中抽取10袋,剔除特级品后,再从剩余土豆中任意抽取两袋,求抽取的两袋都是一等品的概率.
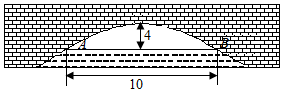 如图,一抛物线型拱桥的拱顶O离水面高4米,水面宽度AB=10米.现有一竹排运送一只货箱欲从桥下经过,已知货箱长20米,宽6米,高2.58米(竹排与水面持平),问货箱能否顺利通过该桥?
如图,一抛物线型拱桥的拱顶O离水面高4米,水面宽度AB=10米.现有一竹排运送一只货箱欲从桥下经过,已知货箱长20米,宽6米,高2.58米(竹排与水面持平),问货箱能否顺利通过该桥?