题目内容
11．已知圆（x-2）2+（y+1）2=16的一条直径恰好经过直线x-2y-3=0被圆所截弦的中点，则该直径所在直线的方程为（ ）| A． | x-2y=0 | B． | 2x+y-5=0 | C． | 2x+y-3=0 | D． | x-2y+4=0 |
分析 由圆的标准方程确定圆心坐标，根据直径和直线的位置关系进行求解即可．
解答 解：由圆（x-2）2+（y+1）2=16，得圆心坐标为（2，-1），
∵圆的一条直径过直线x-2y-3=0被圆截得的弦的中点，
∴直径和直线x-2y-3=0垂直，则直径对应直线的斜率为-2，
则直径所在的直线方程为y+1=-2（x-2），即2x+y-3=0，
故选：C．
点评 本题主要考查直线方程的求解，根据直线和圆的位置关系得到直径和直线垂直是解决本题的关键，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
2．已知函数y=f（x）是R上的偶函数，设a=ln$\frac{1}{π}$，b=（lnπ）2，c=ln$\sqrt{π}$，当任意x1、x2∈（0，+∞）时，都有（x1-x2）•[f（x1）-f（x2）]＜0，则（ ）
| A． | f（a）＞f（b）＞f（c） | B． | f（b）＞f（a）＞f（c） | C． | f（c）＞f（b）＞f（a） | D． | f（c）＞f（a）＞f（b） |
19．阅读如图所示的程序框图，运行相应的程序，则输出的n的值为（ ）
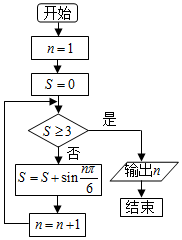
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
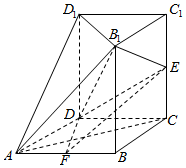如图，几何体ABCD-B1C1D1中，四边形ABCD为菱形，∠BAD=60°，AB=a，平面B1C1D1∥平面ABCD，BB1、CC1、DD1都垂直于平面ABCD，且BB1=$\sqrt{2}$a，E为CC1的中点，F为AB的中点．
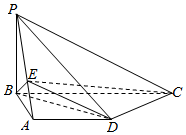如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，AD∥BC，CD⊥BD，PB⊥平面ABCD，PB=AB=AD=3，E是线段PA上一点，且$\frac{PE}{EA}$=λ．