题目内容
12. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,BC∥AD,PA=AB=BC=2,AD=4.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,BC∥AD,PA=AB=BC=2,AD=4.(1)求四棱锥P-ABCD的体积;
2)求证:CD⊥平面PAC.
分析 (1)由四边形ABCD是直角梯形,PA⊥底面ABCD,能求出四棱锥P-ABCD的体积.
(2)由PA⊥底面ABCD,得PA⊥CD,由勾股定理得AC⊥CD,由此能证明CD⊥平面PAC.
解答 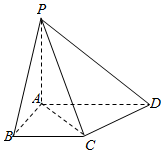 解:(1)由已知,四边形ABCD是直角梯形,
解:(1)由已知,四边形ABCD是直角梯形,
∴${S_{ABCD}}=\frac{1}{2}(2+4)×2=6$,
∵PA⊥底面ABCD,
∴四棱锥P-ABCD的体积${V_{P-ABCD}}=\frac{1}{3}{S_{ABCD}}•PA=\frac{1}{3}×6×2=4$.…(6分)
证明:(2)由PA⊥底面ABCD,CD?底面ABCD,则PA⊥CD,
在三角形ABC中,$AC=\sqrt{A{B^2}+B{C^2}}=2\sqrt{2}$,
又$CD=2\sqrt{2}$,∴AC2+CD2=AD2,即AC⊥CD,…(10分)
又∵PA,AC?平面PAC,PA∩AC=A,
∴CD⊥平面PAC.…(12分)
点评 本题考查线面垂直的证明,考查几何体的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方思想、数形结合思想,是中档题.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
2.命题p“若x=2,则(x-2)(x+1)=0”,其否命题记为q,则下列命题中,真命题是( )
| A. | ¬p | B. | q | C. | p∧q | D. | p∨q |
3.某中学教务处采用系统抽样方法,从学校高一年级全体1000名学生中抽50名学生做学习状况问卷调查.现将1000名学生从1到1000进行编号.在第一组中随机抽取一个号,如果抽到的是17号,则第8组中应取的号码是( )
| A. | 177 | B. | 417 | C. | 157 | D. | 367 |
7.当复数$z=\frac{{{m^2}+m-6}}{m}+({m^2}-2m)i$为纯虚数时,则实数m的值为( )
| A. | m=2 | B. | m=-3 | C. | m=2或m=-3 | D. | m=1或m=-3 |
4.已知下列各式:①f(|x|+1)=x2+1; ②$f(\frac{1}{{{x^2}+1}})=x$;③f(x2-2x)=|x|; ④f(|x|)=3x+3-x.其中存在函数f(x)对任意的x∈R都成立的是( )
| A. | ①④ | B. | ③④ | C. | ①② | D. | ①③ |
1.已知函数f(x)的定义域为[0,2],则函数g(x)=$\frac{f(2x)}{x-1}$的定义域为( )
| A. | [0,1)∪(1,4] | B. | [0,1) | C. | (-∞,1)∪(1,+∞) | D. | [0,1)∪(1,2] |
13.一组数据如表:
(1)画出散点图;
(2)根据下面提供的参考公式,求出回归直线方程,并估计当x=8时,y的值.
(参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
| x | 1 | 2 | 3 | 4 | 5 |
| y | 1.3 | 1.9 | 2.5 | 2.7 | 3.6 |
(2)根据下面提供的参考公式,求出回归直线方程,并估计当x=8时,y的值.
(参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)