题目内容
已知函数f(x)=
x3-
ax2+2x+1(a∈R).
(Ⅰ)若函数f(x)在R上单调递增,求a的取值范围;
(Ⅱ)在(Ⅰ)的条件下,设函数g(x)=ex(ex+a),x∈[0,ln2],求g(x)的最小值.
| 1 |
| 3 |
| 1 |
| 2 |
(Ⅰ)若函数f(x)在R上单调递增,求a的取值范围;
(Ⅱ)在(Ⅰ)的条件下,设函数g(x)=ex(ex+a),x∈[0,ln2],求g(x)的最小值.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)先求导,再根据二次函数恒大于等于0,即△=a2-8≤0,解得即可.
(Ⅱ)先求导,再根据a的范围经行分类讨论,即可求出函数的最小值.
(Ⅱ)先求导,再根据a的范围经行分类讨论,即可求出函数的最小值.
解答:
解:(Ⅰ)求导得:f'(x)=x2-ax+2,
∵函数f(x)在R上单调递增
∴f'(x)≥0恒成立
即x2-ax+2≥0恒成立,于是△=a2-8≤0,
解得:-2
≤a≤2
,
故a的取值范围为[-2
,2
],
(Ⅱ)求导得:g'(x)=ex(2ex+a),
由于0≤x≤ln2,
所以1≤ex≤2,
即2≤2ex≤4,
即a+2≤2ex+a≤a+4,
由(Ⅰ)可知:-2
≤a≤2
,
于是a+4>0
①当a+2≥0即-2≤a≤2
时,即g'(x)≥0,
此时函数g(x)在[0,ln2]上单调递增,所以gmin(x)=g(0)=1+a
②当a+2<0<a+4即-2
≤a<-2时,
令g'(x)=0,即2ex+a=0,解得x=ln(-
a),
此时函数g(x)在[0,ln(-
a)]上单调递减,在[ln(-
a),ln2]上单调递增
所以gmin(x)=g(ln(-
a))=-
a(-
a+a)=-
a2
综上所述:当-2≤a≤2
时,gmin(x)=1+a;当-2
≤a<-2时,gmin(x)═-
a2.
∵函数f(x)在R上单调递增
∴f'(x)≥0恒成立
即x2-ax+2≥0恒成立,于是△=a2-8≤0,
解得:-2
| 2 |
| 2 |
故a的取值范围为[-2
| 2 |
| 2 |
(Ⅱ)求导得:g'(x)=ex(2ex+a),
由于0≤x≤ln2,
所以1≤ex≤2,
即2≤2ex≤4,
即a+2≤2ex+a≤a+4,
由(Ⅰ)可知:-2
| 2 |
| 2 |
于是a+4>0
①当a+2≥0即-2≤a≤2
| 2 |
此时函数g(x)在[0,ln2]上单调递增,所以gmin(x)=g(0)=1+a
②当a+2<0<a+4即-2
| 2 |
令g'(x)=0,即2ex+a=0,解得x=ln(-
| 1 |
| 2 |
此时函数g(x)在[0,ln(-
| 1 |
| 2 |
| 1 |
| 2 |
所以gmin(x)=g(ln(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
综上所述:当-2≤a≤2
| 2 |
| 2 |
| 1 |
| 4 |
点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,考查分类讨论的数学思想,确定函数的单调性是关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
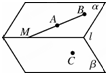 如图,α∩β=l,A,B∈α,C∈β,且C∉l,直线AB∩l=M,过A,B,C三点的平面记作γ,则γ与β的交线必通过( )
如图,α∩β=l,A,B∈α,C∈β,且C∉l,直线AB∩l=M,过A,B,C三点的平面记作γ,则γ与β的交线必通过( )| A、点A | B、点B |
| C、点C但不过点M | D、点C和点M |