题目内容
椭圆C:
+
=1(a>b>0)的离心率为
,两个焦点分别为F1(-1,0),F2(1,0).
(1)求椭圆C的方程;
(2)过点F2(1,0)的直线l交椭圆C于M,N两点,设点N关于x轴的对称点为Q(M、Q不重合),求证:直线MQ过x轴上一个定点.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆C的方程;
(2)过点F2(1,0)的直线l交椭圆C于M,N两点,设点N关于x轴的对称点为Q(M、Q不重合),求证:直线MQ过x轴上一个定点.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)通过椭圆的离心率与焦距,求出a,c,得到b,即可求出椭圆C的方程;
(2)设M(x1,y1),N(x2,y2),Q(x2,-y2),l:y=k(x-1),代入椭圆方程,利用韦达定理,结合MQ的方程为y-y1=
(x-x1),令y=0,化简求解可得x=2,说明直线MQ过x轴上一个定点.
(2)设M(x1,y1),N(x2,y2),Q(x2,-y2),l:y=k(x-1),代入椭圆方程,利用韦达定理,结合MQ的方程为y-y1=
| y1+y2 |
| x1-x2 |
解答:
(本题满分(12分),第(1)问(3分),第(2)问9分)
解:(1)
⇒c=1,a=
,b=1,
所以椭圆的方程为
+y2=1;…(3分)
(2)设M(x1,y1),N(x2,y2),Q(x2,-y2),l:y=k(x-1),
代入
+y2=1(y≠0)整理得(1+2k2)x2-4k2x+2k2-2=0,
由韦达定理可得:x1+x2=
,x1x2=
,…(6分)
MQ的方程为y-y1=
(x-x1)
令y=0,得x=x1+
=x1+
=
代入x1+x2=
,x1x2=
,
x=
=
=2.
得x=2,所以直线过定点(2,0)…(12分)
解:(1)
|
| 2 |
所以椭圆的方程为
| x2 |
| 2 |
(2)设M(x1,y1),N(x2,y2),Q(x2,-y2),l:y=k(x-1),
代入
| x2 |
| 2 |
由韦达定理可得:x1+x2=
| 4k2 |
| 1+2k2 |
| 2k2-2 |
| 1+2k2 |
MQ的方程为y-y1=
| y1+y2 |
| x1-x2 |
令y=0,得x=x1+
| y1(x2-x1) |
| y1+y2 |
| k(x1-1)(x2-x1) |
| k(x1+x2-2) |
| 2x1x2-(x1+x2) |
| x1+x2-2 |
代入x1+x2=
| 4k2 |
| 1+2k2 |
| 2k2-2 |
| 1+2k2 |
x=
| 2x1x2-(x1+x2) |
| x1+x2-2 |
2×
| ||||
|
得x=2,所以直线过定点(2,0)…(12分)
点评:本题考查椭圆方程的求法,直线与椭圆的位置关系的应用,考查转化思想以及计算能力.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
设f(x),g(x)分别是定义在(-∞,0)∪(0,+∞)上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0.且g(-3)=0.则不等式f(x)g(x)<0的解集是( )
| A、(-3,0)∪(3,+∞) |
| B、(-3,0)∪(0,3) |
| C、(-∞,-3)∪(3,+∞) |
| D、(-∞,-3)∪(0,3) |
已知函数f(x)=4x2-mx-8在[5,20]具有单调性,则实数的取值范围为( )
| A、(-∞,-160]∪[160,+∞) |
| B、(-∞,40]∪[160,+∞) |
| C、(-∞,-160]∪[40,+∞) |
| D、[40,160] |
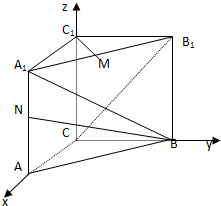 如图,直三棱柱ABC-A1B1C1的底面三角形ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
如图,直三棱柱ABC-A1B1C1的底面三角形ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.