题目内容
设sin2θ=a，cos2θ=b，0＜θ＜
，给出tan(θ+
)值的四个答案：
①
；②
；③
；④
．
其中正确的是 ．
| π |
| 4 |
| π |
| 4 |
①
| b |
| 1-a |
| a |
| 1-b |
| 1+b |
| a |
| 1+a |
| b |
其中正确的是
考点：两角和与差的正切函数
专题：三角函数的求值
分析：由两角和与差的三角函数公式和二倍角公式结合选项验证可得．
解答：
解：∵tan(θ+
)=
=
=
=
=
=
=
=
故答案为：①④
| π |
| 4 |
sin(θ+
| ||
cos(θ+
|
=
| ||||
|
| cosθ+sinθ |
| cosθ-sinθ |
=
| (cosθ+sinθ)2 |
| (cosθ-sinθ)(cosθ+sinθ) |
=
| 1+sin2θ |
| cos2θ |
| cos2θ |
| 1-sin2θ |
=
| b |
| 1-a |
| 1+a |
| b |
故答案为：①④
点评：本题考查两角和与差的三角函数公式，涉及二倍角公式，属基础题．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
已知奇函数f（x）在（-∞，0）上单调递增，且f（2）=0，则不等式（x-1）•f（x-1）＞0的解集是（ ）
| A、（-1，3） |
| B、（-∞-1） |
| C、（-∞-1）∪（3，+∞） |
| D、（-1，1）∪（1，3） |
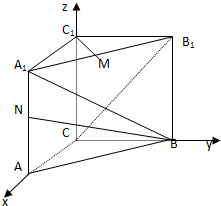如图，直三棱柱ABC-A1B1C1的底面三角形ABC中，CA=CB=1，∠BCA=90°，棱AA1=2，M、N分别是A1B1、A1A的中点．