题目内容
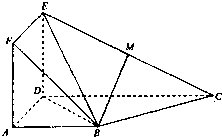 如图,正方形ADEF与梯形ABCD所在的闰面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.
如图,正方形ADEF与梯形ABCD所在的闰面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.(I)求证:BM∥平面ADEF;
(Ⅱ)求平面BEC与平面ADEF所成锐二面角的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:计算题,证明题,转化思想,空间位置关系与距离,空间角
分析:(I)取DE中点N,连接MN,AN,由三角形中位线定理,结合已知中AB∥CD,AB=AD=2,CD=4,易得四边形ABMN为平行四边形,所以BM∥AN,再由线面平面的判定定理,可得BM∥平面ADEF;
(II)以D为原点,DA,DC,DE所在直线为x,y,z轴,建立空间直角坐标系,分别求出平面BEC与平面ADEF的法向量,代入向量夹角公式,即可求出平面BEC与平面ADEF所成锐二面角的余弦值.
(II)以D为原点,DA,DC,DE所在直线为x,y,z轴,建立空间直角坐标系,分别求出平面BEC与平面ADEF的法向量,代入向量夹角公式,即可求出平面BEC与平面ADEF所成锐二面角的余弦值.
解答:
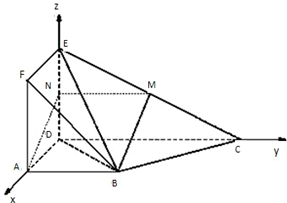 证明:(I)取DE中点N,连接MN,AN
证明:(I)取DE中点N,连接MN,AN
在△EDC中,M、N分别为EC,ED的中点,所以MN∥CD,且MN=
CD.
由已知AB∥CD,AB=
CD,所以MN∥AB,且MN=AB.
所以四边形ABMN为平行四边形,所以BM∥AN
又因为AN?平面ADEF,
且BM?平面ADEF,
所以BM∥平面ADEF.(4分)
(II)以D为原点,DA,DC,DE所在直线为x,y,z轴,建立空间直角坐标系.
B(2,2,0),C(0,4,0),E(0,0,2),平面ADEF的一个法向量为
=(0,1,0).
设
=(x,y,z)为平面BEC的一个法向量,因为
=(-2,2,0),
=(0,-4,2)
∴
令x=1,得y=1,z=2
所以
=(1,1,2)为平面BEC的一个法向量
设平面BEC与平面ADEF所成锐二面角为θ
则cosθ=
=
所以平面BEC与平面ADEF所成锐二面角为余弦值为
 证明:(I)取DE中点N,连接MN,AN
证明:(I)取DE中点N,连接MN,AN在△EDC中,M、N分别为EC,ED的中点,所以MN∥CD,且MN=
| 1 |
| 2 |
由已知AB∥CD,AB=
| 1 |
| 2 |
所以四边形ABMN为平行四边形,所以BM∥AN
又因为AN?平面ADEF,
且BM?平面ADEF,
所以BM∥平面ADEF.(4分)
(II)以D为原点,DA,DC,DE所在直线为x,y,z轴,建立空间直角坐标系.
B(2,2,0),C(0,4,0),E(0,0,2),平面ADEF的一个法向量为
| m |
设
| n |
| BC |
| CE |
∴
|
所以
| n |
设平面BEC与平面ADEF所成锐二面角为θ
则cosθ=
| ||||
|
|
| ||
| 6 |
所以平面BEC与平面ADEF所成锐二面角为余弦值为
| ||
| 6 |
点评:本题考查的知识点是二面角的平面角及求法,直线与平面平行的判定,平面与平面垂直的判定,熟练掌握空间直线与平面不同位置关系(平行和垂直)的判定定理

练习册系列答案
相关题目
某同学连续郑2次骰子,并依次记下正面朝上的点数分别为x,y,记点P(x,y),则点P落在圆C:x2+y2=16内部的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知直线mx+3y-4=0与圆(x+2)2+y2=5相交于A、B两点,若|AB|=2,则实数m的值为( )
A、
| ||||
B、0或-
| ||||
C、±
| ||||
D、
|
点A(1,2,3)在坐标平面yOz内的射影是点B的坐标是( )
| A、(0,2,3) |
| B、(1,0,3) |
| C、(1,2,0) |
| D、(1,0,0) |
 已知正△ABC的边长为2,
已知正△ABC的边长为2, 某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题: