题目内容
函数f(x)是定义在R上的偶函数,且对任意实数x,都有f(x+1)=f(x-1)成立.已知当x∈[1,2]时,f(x)=logax.
(1)求x∈[-1,1]时,函数f(x)的表达式;
(2)若函数f(x)的最大值为
,在区间[-1,3]上,解关于x的不等式f(x)>
.
(1)求x∈[-1,1]时,函数f(x)的表达式;
(2)若函数f(x)的最大值为
| 1 |
| 2 |
| 1 |
| 4 |
考点:其他不等式的解法,函数解析式的求解及常用方法
专题:不等式的解法及应用
分析:(1)由已知中f(x+1)=f(x-1),故可能函数是以2为周期的周期函数,又由函数f(x)是定义在R上的偶函数,结合当x∈[1,2]时,f(x)=logax,我们易得,x∈[-1,1]时,函数f(x)的表达式.
(2)由于f(x)=logax的底数不确定,故我们要对底数进行分类讨论,进而求出满足条件的a值,易将不等式转化为一个对数不等式,根据对数函数的单调性,我们易求出满足条件的不等式的解集.
(2)由于f(x)=logax的底数不确定,故我们要对底数进行分类讨论,进而求出满足条件的a值,易将不等式转化为一个对数不等式,根据对数函数的单调性,我们易求出满足条件的不等式的解集.
解答:
解:(1)由函数f(x)是定义在R上的偶函数,且f(x+1)=f(x-1)成立,
可得f(x+2)=f(x),∴f(x)=
.
(2)由于函数是以2为周期的周期函数,故只需要考查区间[-1,1]
当a>1时,由函数f(x)的最大值为
,知f(0)=f(x)max=loga2=
,即a=4.
当0<a<1时,则当x=±1时,函数f(x)取最大值为
即loga(2-1)=
,舍去.
综上所述,a=4.
当x∈[-1,1]时,若x∈[-1,0],则由log4(2+x)>
,可得
-2<x≤0.
若x∈(0,1],则由log4(2-x)>
,可得0<x<2-
.
∴此时满足不等式的解集为(
-2,2-
).
∵函数是以2为周期的周期函数,∴在区间[-1,3]上,f(x)>
的解集为(
,4-
).
综上,所得不等式的解集为(
-2,2-
)∪(
,4-
).
可得f(x+2)=f(x),∴f(x)=
|
(2)由于函数是以2为周期的周期函数,故只需要考查区间[-1,1]
当a>1时,由函数f(x)的最大值为
| 1 |
| 2 |
| 1 |
| 2 |
当0<a<1时,则当x=±1时,函数f(x)取最大值为
| 1 |
| 2 |
| 1 |
| 2 |
综上所述,a=4.
当x∈[-1,1]时,若x∈[-1,0],则由log4(2+x)>
| 1 |
| 4 |
| 2 |
若x∈(0,1],则由log4(2-x)>
| 1 |
| 4 |
| 2 |
∴此时满足不等式的解集为(
| 2 |
| 2 |
∵函数是以2为周期的周期函数,∴在区间[-1,3]上,f(x)>
| 1 |
| 4 |
| 2 |
| 2 |
综上,所得不等式的解集为(
| 2 |
| 2 |
| 2 |
| 2 |
点评:本题考查的知识点是函数奇偶性与单调性的综合应用,函数的周期性,其中当对数函数的底数不确定时,对a进行分类讨论是对数函数常用的处理的方法,属于中档题.

练习册系列答案
相关题目
如果a
=b(a>0,且a≠1),则( )
| 1 |
| 2 |
A、log
| ||||
B、log
| ||||
C、log
| ||||
D、log
|
已知
ax不存在(a>0),则
的值为( )
| lim |
| x→∞ |
| lim |
| x→∞ |
| 1-ax |
| 1+ax |
| A、-1 | B、0 | C、1 | D、不存在 |
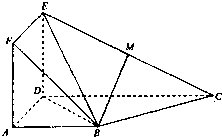 如图,正方形ADEF与梯形ABCD所在的闰面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.
如图,正方形ADEF与梯形ABCD所在的闰面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.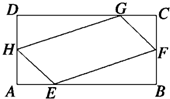 如图所示,在矩形ABCD中,已知AB=a,BC=b(b<a),AB,AD,CD,CB上分别截取AE,AH,CG,CF都等于x,记四边形EFGH的面积为f(x).
如图所示,在矩形ABCD中,已知AB=a,BC=b(b<a),AB,AD,CD,CB上分别截取AE,AH,CG,CF都等于x,记四边形EFGH的面积为f(x).