题目内容
已知直线mx+3y-4=0与圆(x+2)2+y2=5相交于A、B两点,若|AB|=2,则实数m的值为( )
A、
| ||||
B、0或-
| ||||
C、±
| ||||
D、
|
考点:直线与圆的位置关系
专题:直线与圆
分析:根据圆的标准方程找出圆心坐标与半径,利用垂径定理及勾股定理求出弦心距的长,即为圆心到直线的距离,利用点到直线的距离公式列出关于m的方程,求出方程的解即可得到m的值.
解答:
解:∵(x+2)2+y2=5,
∴圆心坐标为(-2,0),半径r=
,
∵|AB|=2,
∴圆心到直线的距离d=
=
=2,
即(2m+4)2=4(m2+9),
解得:m=
.
故选D
∴圆心坐标为(-2,0),半径r=
| 5 |
∵|AB|=2,
∴圆心到直线的距离d=
| |-2m-4| | ||
|
r2-(
|
即(2m+4)2=4(m2+9),
解得:m=
| 5 |
| 4 |
故选D
点评:此题考查了直线与圆的位置关系,涉及的知识有:点到直线的距离公式,垂径定理,勾股定理,以及圆的标准方程,熟练掌握垂径定理及勾股定理是解本题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
如果a
=b(a>0,且a≠1),则( )
| 1 |
| 2 |
A、log
| ||||
B、log
| ||||
C、log
| ||||
D、log
|
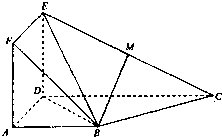 如图,正方形ADEF与梯形ABCD所在的闰面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.
如图,正方形ADEF与梯形ABCD所在的闰面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.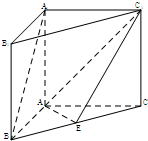 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.