题目内容
点A（1，2，3）在坐标平面yOz内的射影是点B的坐标是（ ）
| A、（0，2，3） |
| B、（1，0，3） |
| C、（1，2，0） |
| D、（1，0，0） |
考点：空间中的点的坐标
专题：计算题
分析：要求点A（1，2，3）在yOz坐标平面内的射影点B的坐标，通过A与B的纵标和竖标相同，横标为0，得到B的坐标即可．
解答：
解：∵点B是A（1，2，3）在yOz坐标平面内的射影
∴A与B的纵标和竖标相同，横标为0，得到B的坐标（0，2，3）．
故选A．
∴A与B的纵标和竖标相同，横标为0，得到B的坐标（0，2，3）．
故选A．
点评：本题考查空间直角坐标系，考查空间中点的坐标关系，解题的关键是，空间直角坐标系的理解是否到位．
练习册系列答案
春雨教育同步作文系列答案
相关题目
函数f（x）=lg（3+2x-x2）的定义域是（ ）
| A、（-∞，-1）∪（3，+∞） |
| B、（-∞，-3）∪（1，+∞） |
| C、（-3，1） |
| D、（-1，3） |
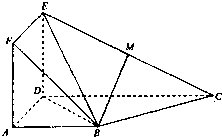如图，正方形ADEF与梯形ABCD所在的闰面互相垂直，AD⊥CD，AB∥CD，AB=AD=2，CD=4，M为CE的中点．已知
ax不存在(a＞0)，则
的值为（ ）
| lim |
| x→∞ |
| lim |
| x→∞ |
| 1-ax |
| 1+ax |
| A、-1 | B、0 | C、1 | D、不存在 |