题目内容
在极坐标系中，过圆ρ=4cosθ的圆心，且垂直于极轴的直线的极坐标方程为 ．
考点：简单曲线的极坐标方程
专题：计算题
分析：先将原极坐标方程ρ=4cosθ的两边同乘以ρ后化成直角坐标方程，再利用直角坐标方程进行求解即可．
解答：
解：由题意可知圆的标准方程为：
（x-2）2+y2=9，圆心是（2，0），
所求直线普通方程为x=2，
则极坐标方程为ρcosθ=2．
故答案为：ρcosθ=2．
（x-2）2+y2=9，圆心是（2，0），
所求直线普通方程为x=2，
则极坐标方程为ρcosθ=2．
故答案为：ρcosθ=2．
点评：本题考查点的极坐标和直角坐标的互化，利用直角坐标与极坐标间的关系，即利用ρcosθ=x，ρsinθ=y，ρ2=x2+y2，进行代换即得．
练习册系列答案
相关题目
一个几何体的三视图如图所示，则该几何体的表面积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f（x）=lg（3+2x-x2）的定义域是（ ）
| A、（-∞，-1）∪（3，+∞） |
| B、（-∞，-3）∪（1，+∞） |
| C、（-3，1） |
| D、（-1，3） |
已知点P是边长为2的线段AB上任意一点，则PA＞PB的概率为（ ）
| A、1 | ||
B、
| ||
| C、0.5 | ||
D、
|
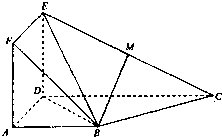如图，正方形ADEF与梯形ABCD所在的闰面互相垂直，AD⊥CD，AB∥CD，AB=AD=2，CD=4，M为CE的中点．