题目内容
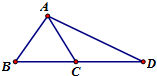已知正△ABC的边长为2，| BD |
| BC |
| AD |
| AC |
考点：平面向量数量积的运算,向量在几何中的应用
专题：平面向量及应用
分析：由向量的运算可得
=
+
，
=
+
，代入可化为关于向量
，
的运算式，由已知条件易得结果，注意向量
与
的夹角为120°
| AD |
| AB |
| BD |
| AC |
| AB |
| BC |
| AB |
| BC |
| AB |
| BC |
解答：
解：由题意可得
•
=（
+
）•（
+
）
=（
+4
）•（
+
）=
2+5
•
+4
2
=22+5×2×2×cos120°+4×22=10，
故答案为：10
| AD |
| AC |
| AB |
| BD |
| AB |
| BC |
=（
| AB |
| BC |
| AB |
| BC |
| AB |
| AB |
| BC |
| BC |
=22+5×2×2×cos120°+4×22=10，
故答案为：10
点评：本题考查平面向量数量积的运算，用向量
，
来表示向量是解决问题的关键，属中档题．
| AB |
| BC |
练习册系列答案
特高级教师点拨系列答案
相关题目
函数f（x）=
，则函数y=f（x）-x的零点个数为（ ）
|
| A、2 | B、3 | C、4 | D、无数 |
函数f（x）=lg（3+2x-x2）的定义域是（ ）
| A、（-∞，-1）∪（3，+∞） |
| B、（-∞，-3）∪（1，+∞） |
| C、（-3，1） |
| D、（-1，3） |
如图，AB为半圆的直径，P为半圆上一点，|AB|=10，∠PAB=a，且sina=已知点P是边长为2的线段AB上任意一点，则PA＞PB的概率为（ ）
| A、1 | ||
B、
| ||
| C、0.5 | ||
D、
|
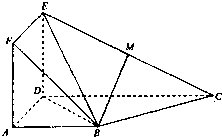如图，正方形ADEF与梯形ABCD所在的闰面互相垂直，AD⊥CD，AB∥CD，AB=AD=2，CD=4，M为CE的中点．