题目内容
 某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:频率分布表
| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 8 | 0.16 |
| 第2组 | [60,70) | a | ▓ |
| 第3组 | [70,80) | 20 | 0.40 |
| 第4组 | [80,90) | ▓ | 0.08 |
| 第5组 | [90,100] | 2 | b |
| 合计 | ▓ | ▓ |
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动,求所抽取的2名同学来自同一组的概率;
(3)在(2)的条件下,设ξ表示所抽取的2名同学中来自第5组的人数,求ξ的分布列及其数学期望.
考点:离散型随机变量的期望与方差,频率分布直方图
专题:概率与统计
分析:(1)利用频率=
×100%,及
表示频率分布直方图的纵坐标即可求出a,b,x,y;
(2)由(1)可知第四组的人数,已知第五组的人数是2,利用组合的计算公式即可求出从这6人中任选2人的种数,再分两类分别求出所选的两人来自同一组的情况,利用互斥事件的概率和古典概型的概率计算公式即可得出;
(3)由(2)可知,ξ的可能取值为0,1,2,再利用组合的计算公式及古典概型的计算公式、数学期望的计算公式即可得出.
| 频数 |
| 样本容量 |
| 频率 |
| 组距 |
(2)由(1)可知第四组的人数,已知第五组的人数是2,利用组合的计算公式即可求出从这6人中任选2人的种数,再分两类分别求出所选的两人来自同一组的情况,利用互斥事件的概率和古典概型的概率计算公式即可得出;
(3)由(2)可知,ξ的可能取值为0,1,2,再利用组合的计算公式及古典概型的计算公式、数学期望的计算公式即可得出.
解答:
解:(1)由题意可知,样本容量=
=50,∴b=
=0.04,
第四组的频数=50×0.08=4,
∴a=50-8-20-2-4=16.
y=
=0.004,x=
×
=0.032.
∴a=16,b=0.04,x=0.032,y=0.004.
(2)由(1)可知,第4组有4人,第5组有2人,共6人.
从竞赛成绩是80分)以上(含80分)的同学中随机抽取2名同学有
=15种情况.
设事件A:随机抽取的2名同学来自同一组,则P(A)=
=
.
所以,随机抽取的2名同学来自同一组的概率是
.
(3)由(2)可知,ξ的可能取值为0,1,2,
则P(ξ=0)=
=
=
,P(ξ=1)=
=
,P(ξ=2)=
=
.
所以,ξ的分布列为
所以,Eξ=0×
+1×
+2×
=
.
| 8 |
| 0.16 |
| 2 |
| 50 |
第四组的频数=50×0.08=4,
∴a=50-8-20-2-4=16.
y=
| 0.04 |
| 10 |
| 16 |
| 50 |
| 1 |
| 10 |
∴a=16,b=0.04,x=0.032,y=0.004.
(2)由(1)可知,第4组有4人,第5组有2人,共6人.
从竞赛成绩是80分)以上(含80分)的同学中随机抽取2名同学有
| C | 2 6 |
设事件A:随机抽取的2名同学来自同一组,则P(A)=
| ||||
|
| 7 |
| 15 |
所以,随机抽取的2名同学来自同一组的概率是
| 7 |
| 15 |
(3)由(2)可知,ξ的可能取值为0,1,2,
则P(ξ=0)=
| ||
|
| 6 |
| 15 |
| 2 |
| 5 |
| ||||
|
| 8 |
| 15 |
| ||
|
| 1 |
| 15 |
所以,ξ的分布列为
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 2 |
| 5 |
| 8 |
| 15 |
| 1 |
| 15 |
| 2 |
| 3 |
点评:熟练掌握频率=
×100%,及
表示频率分布直方图的纵坐标、频率之和等于1、互斥事件的概率、组合的计算公式及古典概型的计算公式、数学期望的计算公式是解题的关键.
| 频数 |
| 样本容量 |
| 频率 |
| 组距 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设全集I=R,T={x|x2<x},M={x|x∉T},则M等于( )
| A、{x|x≥1} |
| B、{x|x>1} |
| C、{x|-1≤x≤0} |
| D、{x|x≥1或x≤0} |
已知A,B,C为圆O上三点,线段CO的延长线与线段AB有交点,若
=m
+n
,则m+n的范围是( )
| OC |
| OA |
| OB |
| A、(0,1) |
| B、(1,+∞) |
| C、(-1,0) |
| D、(-∞,-1) |
 如图,AB为半圆的直径,P为半圆上一点,|AB|=10,∠PAB=a,且sina=
如图,AB为半圆的直径,P为半圆上一点,|AB|=10,∠PAB=a,且sina=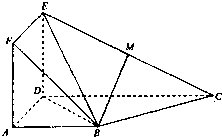 如图,正方形ADEF与梯形ABCD所在的闰面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.
如图,正方形ADEF与梯形ABCD所在的闰面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.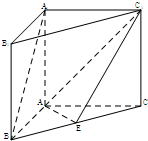 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=2,E是BC中点.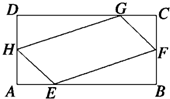 如图所示,在矩形ABCD中,已知AB=a,BC=b(b<a),AB,AD,CD,CB上分别截取AE,AH,CG,CF都等于x,记四边形EFGH的面积为f(x).
如图所示,在矩形ABCD中,已知AB=a,BC=b(b<a),AB,AD,CD,CB上分别截取AE,AH,CG,CF都等于x,记四边形EFGH的面积为f(x).