题目内容
若函数y=f(x)在区间[a,b]上的图象为连续不断的一条曲线,则下列说法正确的是( )
| A、若f(a)f(b)>0,不存在实数c∈(a,b)使得f(c)=0 |
| B、若f(a)f(b)>0,有可能存在实数c∈(a,b)使得f(c)=0 |
| C、若f(a)f(b)<0,存在且只存在一个实数c∈(a,b)使得f(c)=0 |
| D、若f(a)f(b)<0,有可能不存在实数c∈(a,b)使得f(c)=0 |
考点:函数的图象
专题:函数的性质及应用
分析:画满足条件的函数图象排除不正确的选项
解答:
解:首先,设函数y=f(x)在区间[a,b]上的图象如下图:

上图满足f(a)f(b)>0,有可能存在实数c∈(a,b)使得f(c)=0,故A错误,B正确;
其次,设函数y=f(x)在区间[a,b]上的图象如下图:

上图满足f(a)f(b)<0,但C都错误,
D、根据零点存在定理,一定存在实数c∈(a,b)使得f(c)=0,所以D错误,
故选:B.

上图满足f(a)f(b)>0,有可能存在实数c∈(a,b)使得f(c)=0,故A错误,B正确;
其次,设函数y=f(x)在区间[a,b]上的图象如下图:

上图满足f(a)f(b)<0,但C都错误,
D、根据零点存在定理,一定存在实数c∈(a,b)使得f(c)=0,所以D错误,
故选:B.
点评:本题主要考查函数零点存在定理,画函数的图象研究函数的性质是常见的方法,突出说明数形结合思想的重要性.

练习册系列答案
相关题目
把1,3,6,10,15,21这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形(如图所示).则第七个三角形数是( )
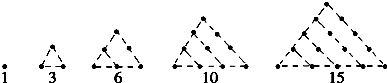

| A、27 | B、28 | C、29 | D、30 |
一个几何体的三视图如图所示,则该几何体的体积是( )


A、128
| ||||
B、
| ||||
| C、128 | ||||
D、
|
设函数f(x)=|x+1|+|x-a|的图象关于直线x=2对称,则a的值为( )
| A、5 | B、-5 | C、3 | D、-3 |
x+
(x>0)的最小值是( )
| 4 |
| x |
| A、2 | ||
B、2
| ||
| C、4 | ||
| D、8 |
圆C1:x2+y2+2x=0与圆C2:x2+y2-4x+8y+4=0的位置关系是( )
| A、相交 | B、外切 | C、内切 | D、相离 |