题目内容
把1,3,6,10,15,21这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形(如图所示).则第七个三角形数是( )
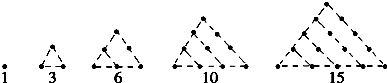

| A、27 | B、28 | C、29 | D、30 |
考点:归纳推理
专题:推理和证明
分析:原来三角形数是从l开始的连续自然数的和.l是第一个三角形数,3是第二个三角形数,6是第三个三角形数,10是第四个三角形数,15是第五个三角形数…那么,第七个三角形数就是:l+2+3+4+5+6+7=28.
解答:
解:原来三角形数是从l开始的连续自然数的和.
l是第一个三角形数,第1个数是1;
3是第二个三角形数,第2个数是3=1+2;
6是第三个三角形数,第3个数是:6=1+2+3;
10是第四个三角形数,第4个数是:10=1+2+3+4;
15是第五个三角形数,第5个数是:15=1+2+3+4+5;
…
那么,第七个三角形数就是:l+2+3+4+5+6+7=28.
故选:B.
l是第一个三角形数,第1个数是1;
3是第二个三角形数,第2个数是3=1+2;
6是第三个三角形数,第3个数是:6=1+2+3;
10是第四个三角形数,第4个数是:10=1+2+3+4;
15是第五个三角形数,第5个数是:15=1+2+3+4+5;
…
那么,第七个三角形数就是:l+2+3+4+5+6+7=28.
故选:B.
点评:本题考查数列在生产实际中的应用,考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,易出错,是高考的重点.解题时要认真审题,注意总结规律,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若函数Mf(a,b)的图象如图所示,则下列函数图象正确的是( )


A、 |
B、 |
C、 |
D、 |
椭圆的两个焦点和中心把两准线间的距离四等分,则一焦点与短轴两端点连线的夹角是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
从1,3,5,7,9这5个数中任取3个,这三个数能成为三角形三边的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数y=f(x)在区间[a,b]上的图象为连续不断的一条曲线,则下列说法正确的是( )
| A、若f(a)f(b)>0,不存在实数c∈(a,b)使得f(c)=0 |
| B、若f(a)f(b)>0,有可能存在实数c∈(a,b)使得f(c)=0 |
| C、若f(a)f(b)<0,存在且只存在一个实数c∈(a,b)使得f(c)=0 |
| D、若f(a)f(b)<0,有可能不存在实数c∈(a,b)使得f(c)=0 |
若一直线过M(0,-1)且被圆(x-1)2+(y-2)2=25截得的弦AB长为8,则这条直线的方程是( )
| A、3x+4y+4=0 |
| B、3x+4y+4=0或y+1=0 |
| C、3x-4y-4=0 |
| D、3x-4y-4=0或y+1=0 |