题目内容
数列{an}满足,a1=2,an+1=
,(n∈N*)其前n项积为Tn,则T2014= .
| 1+an |
| 1-an |
考点:数列递推式
专题:综合题,点列、递归数列与数学归纳法
分析:根据数列{an}满足a1=2,an+1=
(n∈N*),可得数列{an}是周期为4的周期数列,且a1a2a3a4=1,即可得出结论.
| 1+an |
| 1-an |
解答:
解:∵a1=2,an+1=
(n∈N*),
∴a2=-3,a3=-
,a4=
,a5=2,…,
∴数列{an}是周期为4的周期数列,且a1a2a3a4=1,
∵2014=4×503+2,
∴T2014=-6.
故答案为:-6
| 1+an |
| 1-an |
∴a2=-3,a3=-
| 1 |
| 2 |
| 1 |
| 3 |
∴数列{an}是周期为4的周期数列,且a1a2a3a4=1,
∵2014=4×503+2,
∴T2014=-6.
故答案为:-6
点评:本题考查数列递推式,考查学生分析解决问题的能力,确定数列{an}是周期为4的周期数列,且a1a2a3a4=1是关键.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
已知如图所示的程序框图,当输入n=99时,输出S的值( )


A、
| ||
B、
| ||
C、
| ||
D、
|
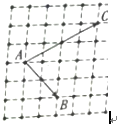 如图所示的方格纸上有三个点A,B,C,且每个小方格的边长为1.
如图所示的方格纸上有三个点A,B,C,且每个小方格的边长为1.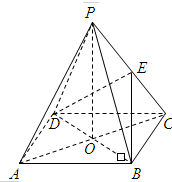 如图,四棱锥P-ABCD是正方形,边长为2,O是正方形的中心,PO⊥底面ABCD,E是PC的中点,且该四棱锥的侧棱长都是3.
如图,四棱锥P-ABCD是正方形,边长为2,O是正方形的中心,PO⊥底面ABCD,E是PC的中点,且该四棱锥的侧棱长都是3.