题目内容

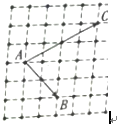如图所示的方格纸上有三个点A，B，C，且每个小方格的边长为1．
（1）求向量
BC
的模；
（2）求向量
AB
和向量
AC
夹角的余弦值．
考点：数量积表示两个向量的夹角
专题：平面向量及应用
分析：（1）由题意求得
AB
、
AC
 的坐标，可得  
BC
=
AC
-
AB
 的坐标，从而求得|
BC
|．
（2）设向量
AB
和向量
AC
夹角为θ，则由cosθ=
AB
•
AC
|
AB
|•|
AC
|
 计算求得结果．
解答： 解：（1）由题意可得
AB
=（2，-3）
AC
=（ 4，2），
∴
BC
=
AC
-
AB
=（2，5），故|
BC
|=
22+52
=
29
．
（2）设向量
AB
和向量
AC
夹角为θ，则cosθ=
AB
•
AC
|
AB
|•|
AC
|
=
2×4+(-3)×2
13
•
20
=
65
65
．
点评：本题主要考查两个向量的夹角公式的应用，求向量的模的方法，两个向量坐标形式的运算，属于基础题．
练习册系列答案
相关题目
某同学“期末”考试各科成绩都在“期中”考试的基础上提高了2分，则该同学成绩的（　　）
A、中位数不变B、极差变大
C、方差不变D、标准差变大
已知椭圆C：x2+2y2=4．则椭圆C的离心率是
 
．
若a=log3π，b=0.52013，c=log20130.5，则a，b，c的大小关系是
 
．
已知函数f（x）=a+
1
2x-1
（a∈R）是奇函数．
（1）求a的值；
（2）讨论函数f（x）在（0，+∞）上的单调性，并求函数f（x）在[1，t]上的最大值和最小值．
数列{an}满足，a1=2，an+1=
1+an
1-an
，（n∈N*）其前n项积为Tn，则T2014=
 
．
设函数f（x）=sin2x+cos（2x+
π
3
）
（Ⅰ）求函数f（x）的最大值及此时x的取值集合；
（Ⅱ）设A，B，C为△ABC的三个内角，若cosB=
1
3
，f（
C
2
）=-
1
4
，且C为锐角，求sinA的值．
（文）（1）设命题p：若a≥0，则x2+x-a=0有实根．试写出命题p的逆否命题并判断真假；
（2）设命题p：函数y=kx+1在R上是增函数，命题q：曲线y=x2+（2k-3）x+1与x轴交于不同的两点，如果p∧q是真命题，求k的取值范围．
已知数列{an}的通项公式an=2n，n∈N*，则
.
a1a2
a3a4
.
+
.
a2a3
a4a5
.
+
.
a3a4
a5a6
.
++
.
a2012a2013
a2014a2015
.
=（　　）
A、-16096
B、-16104
C、-16112
D、-16120

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网