题目内容
已知S-ABCD是一个底面边长为4
,高为3的正四棱锥.在S-ABCD内任取一点P,则四棱锥P-ABCD的体积大于16的概率为 .
| 2 |
考点:几何概型
专题:概率与统计
分析:求出四棱锥P-ABCD的体积等于16时,对应的高,利用体积之间的关系即可得到结论.
解答:
解:∵S-ABCD是一个底面边长为4
,高为3的正四棱锥.
∴正四棱锥S-ABCD的体积为
×(4
)2×3=32,
若四棱锥P-ABCD的体积16,则四棱锥P-ABCD的高为h,
则满足
×(4
)2h=16,
解得h=
,
则两个棱锥的体积比等于对应高的立方比,
即四棱锥P-ABCD的体积大于16的概率P=
=(
)3=
,
故答案为:
| 2 |
∴正四棱锥S-ABCD的体积为
| 1 |
| 3 |
| 2 |
若四棱锥P-ABCD的体积16,则四棱锥P-ABCD的高为h,
则满足
| 1 |
| 3 |
| 2 |
解得h=
| 3 |
| 2 |
则两个棱锥的体积比等于对应高的立方比,
即四棱锥P-ABCD的体积大于16的概率P=
| VP-ABCD |
| VS-ABCD |
| ||
| 3 |
| 1 |
| 8 |
故答案为:
| 1 |
| 8 |
点评:本题主要考查几何槪型的概率的计算,利用体积之间的关系是解决本题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目

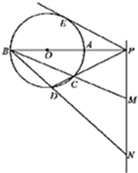 如图,已知PE是⊙O的切线,切点为E,PAB,PCD都是⊙O的割线,且PAB经过圆心O,过点P直线与直线BC,BD分别交于点M,N,且PE2=PM•PN.
如图,已知PE是⊙O的切线,切点为E,PAB,PCD都是⊙O的割线,且PAB经过圆心O,过点P直线与直线BC,BD分别交于点M,N,且PE2=PM•PN.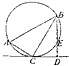 如图,在△ABC中,∠C=90°,∠A=60°,AB=10,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则线段BE的长为
如图,在△ABC中,∠C=90°,∠A=60°,AB=10,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则线段BE的长为