题目内容
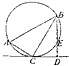 如图,在△ABC中,∠C=90°,∠A=60°,AB=10,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则线段BE的长为
如图,在△ABC中,∠C=90°,∠A=60°,AB=10,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则线段BE的长为考点:与圆有关的比例线段
专题:计算题,立体几何
分析:利用直角△ABC的边角关系即可得出BC,利用弦切角定理可得∠BCD=∠A=60°.利用直角△BCD的边角关系即可得出CD,BD.再利用切割线定理可得CD2=DE•DB,即可得出BE.
解答:
解:在△ABC中,∠C=90°,∠A=60°,AB=10,∴BC=AB•sin60°=5
.
∵CD是此圆的切线,∴∠BCD=∠A=60°.
在Rt△BCD中,CD=BC•cos60°=
,BD=BC•sin60°=
.
由切割线定理可得CD2=DE•DB,∴(
)2=(
-BE)•
,解得BE=5.
故答案为:5.
| 3 |
∵CD是此圆的切线,∴∠BCD=∠A=60°.
在Rt△BCD中,CD=BC•cos60°=
5
| ||
| 2 |
| 15 |
| 2 |
由切割线定理可得CD2=DE•DB,∴(
5
| ||
| 2 |
| 15 |
| 2 |
| 15 |
| 2 |
故答案为:5.
点评:熟练掌握直角三角形的边角关系、弦切角定理、切割线定理是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目