题目内容
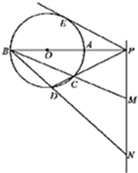如图，已知PE是⊙O的切线，切点为E，PAB，PCD都是⊙O的割线，且PAB经过圆心O，过点P直线与直线BC，BD分别交于点M，N，且PE2=PM•PN．（Ⅰ）求证D，C，M，N四点共圆；
（Ⅱ）求证PB⊥PN．
考点：与圆有关的比例线段,圆內接多边形的性质与判定
专题：选作题,立体几何
分析：（Ⅰ）证明D，C，M，N四点共圆，只需证明∠DCM+∠PND=180°；
（Ⅱ）证明PB⊥PN，只需证明∠BPN=90°，由圆周角定理可证．
（Ⅱ）证明PB⊥PN，只需证明∠BPN=90°，由圆周角定理可证．
解答：
证明：（Ⅰ）∵PE是⊙O的切线，∴PE2=PC•PD，
又∵PE2=PM•PN，
∴
=
，
又∵∠CPM=∠NPD，
∴△PCM∽△PND，
∴∠PCM=∠PND，
∴∠DCM+∠PND=180°，
∴D，C，M，N四点共圆．---------（5分）
（Ⅱ）由（Ⅰ）知∠BCD=∠PND，
由圆周角定理得∠BCD+∠NBP=90°，∠PND+∠NBP=90°，
∴∠BPN=90°，∴PB⊥PN．-------------（10分）
又∵PE2=PM•PN，
∴
| PC |
| PM |
| PN |
| PD |
又∵∠CPM=∠NPD，
∴△PCM∽△PND，
∴∠PCM=∠PND，
∴∠DCM+∠PND=180°，
∴D，C，M，N四点共圆．---------（5分）
（Ⅱ）由（Ⅰ）知∠BCD=∠PND，
由圆周角定理得∠BCD+∠NBP=90°，∠PND+∠NBP=90°，
∴∠BPN=90°，∴PB⊥PN．-------------（10分）
点评：本题考查了相似三角形的性质和判定，切割线定理，圆周角定理等知识点的应用，主要考查学生的推理能力，综合性比较强，有一定的难度．
练习册系列答案
培优口算题卡系列答案
相关题目