题目内容
设函数y=f(x)为定义在R上的奇函数,f(x+2)=-f(x).当x∈[-1,0]时,f(x)=f0(x)=x3.
(1)当x∈[1,3]时,求y=f1(x)的解析式;
(2)记y=f(x),x∈(4k-1,4k+1],k∈Z为y=fk(x),求y=fk(x)及其反函数y=fk-1(x)的解析式;
(3)定义g(x)=2k+(-1)kf(x),其中x∈[2k-1,2k+1],探究方程g(x)-b=0(b>0)在区间[-2013,2013]上的解的个数.
(1)当x∈[1,3]时,求y=f1(x)的解析式;
(2)记y=f(x),x∈(4k-1,4k+1],k∈Z为y=fk(x),求y=fk(x)及其反函数y=fk-1(x)的解析式;
(3)定义g(x)=2k+(-1)kf(x),其中x∈[2k-1,2k+1],探究方程g(x)-b=0(b>0)在区间[-2013,2013]上的解的个数.
考点:根的存在性及根的个数判断,函数解析式的求解及常用方法,反函数
专题:函数的性质及应用
分析:(1)转化为[-1,0]时求解,(2)根据反函数概念求解,(3)运用图象求解,分类讨论.
解答:
解:(1)当x∈[0,1]时,-x∈[-1,0],
f(x)=-f(-x)=x3,(-1≤x≤1);
(2)f(x+2)=-f(x),可得.f(x+4)=-f(x+2)=f(x).
则f(x)的周期为4;
当x∈[1,3]时,x-2∈[-1,1],有f(x)=-f(x-2)=-(x-2)3
当x∈[4k-1,4k+1]时,x-4k∈[-1,1],有fk(x)=-f(x-4k)=-(x-4k)3.
x-4k=
,即y=f-1k(x)=4k+
,(-1<x≤1)
(3)由f(x+2)=-f(x)=f(-x)
可得f(x)的对称轴为x=1,所以f(x)的图象如下:
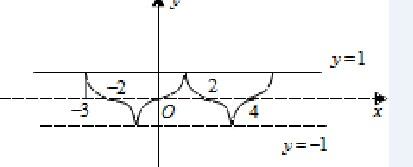
接下来求解f(x)在[2k-1,2k+1]上的解析式:
①当k为偶数时,2k为其周期,x-2k∈[-1,1]
所以f(x)=f(x-2k)=(x-2k)3
②当k为奇数时,2k-2为其周期,x-(2k-2)∈[1,3]
所以f(x)=f(x-2k)=(x-(2k-2))3=-f(x-2k)=-(x-2k)3,
综上f(x)=(-1)k(x-2k)3,
g(x)=2k+(x-2k)3,x∈[2k-1,2k+1],k∈z
所以将y=x3,向右移动2k个单位,再向上移动2k个单位即可得到g(x)的图象;
显然g(x)是连续的递增函数,
∴当0<b≤g(2013)=2013时,
方程g(x)-b=0在区间[-2013,2013]上有一解,
当b>2013时,方程g(x)-b=0,在区间[-2013,2013]上无
f(x)=-f(-x)=x3,(-1≤x≤1);
(2)f(x+2)=-f(x),可得.f(x+4)=-f(x+2)=f(x).
则f(x)的周期为4;
当x∈[1,3]时,x-2∈[-1,1],有f(x)=-f(x-2)=-(x-2)3
当x∈[4k-1,4k+1]时,x-4k∈[-1,1],有fk(x)=-f(x-4k)=-(x-4k)3.
x-4k=
| 3 | y |
| 3 | x |
(3)由f(x+2)=-f(x)=f(-x)
可得f(x)的对称轴为x=1,所以f(x)的图象如下:

接下来求解f(x)在[2k-1,2k+1]上的解析式:
①当k为偶数时,2k为其周期,x-2k∈[-1,1]
所以f(x)=f(x-2k)=(x-2k)3
②当k为奇数时,2k-2为其周期,x-(2k-2)∈[1,3]
所以f(x)=f(x-2k)=(x-(2k-2))3=-f(x-2k)=-(x-2k)3,
综上f(x)=(-1)k(x-2k)3,
g(x)=2k+(x-2k)3,x∈[2k-1,2k+1],k∈z
所以将y=x3,向右移动2k个单位,再向上移动2k个单位即可得到g(x)的图象;
显然g(x)是连续的递增函数,
∴当0<b≤g(2013)=2013时,
方程g(x)-b=0在区间[-2013,2013]上有一解,
当b>2013时,方程g(x)-b=0,在区间[-2013,2013]上无
点评:本题考查了函数的性质,定义,图象运用,属于中档题.

练习册系列答案
相关题目
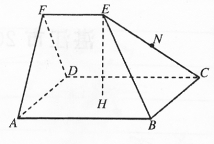 如图,五面体EF-ABCD中,ABCD是以点H为中心的正方形,EF∥AB,EH丄平面 ABCD,AB=2,EF=EH=1.
如图,五面体EF-ABCD中,ABCD是以点H为中心的正方形,EF∥AB,EH丄平面 ABCD,AB=2,EF=EH=1.