题目内容
若α,β是关于x的一元二次方程x2+2(cosθ+1)x+cos2θ=0的两根,且|α-β|≤2
,求θ的范围.
| 2 |
考点:三角函数中的恒等变换应用,根与系数的关系
专题:计算题,不等式的解法及应用
分析:由已知可求得α2+β2=2cos2θ+8cosθ+4,αβ=cos2θ,从而由|α-β|≤2
可求得cosθ≤
,从而可求θ的范围.
| 2 |
| 1 |
| 2 |
解答:
解:若α,β是关于x的一元二次方程x2+2(cosθ+1)x+cos2θ=0的两根,
则有:△=4(cosθ+1)2-4cos2θ=4+8cosθ>0,可得:cosθ>-
,
则有:α+β=-
=-2(cosθ+1);αβ=cos2θ.
故有(α+β)2=α2+β2+2αβ=4(cosθ+1)2=4cos2θ+8cosθ+4,
故:α2+β2=2cos2θ+8cosθ+4
∵|α-β|≤2
,∴(α-β)2≤8,
故α2+β2-2αβ=2cos2θ+8cosθ+4-2cos2θ=8cosθ+4≤8
从而得:cosθ≤
.
故:-
<cosθ≤
故θ的范围为:[2kπ+
,2kπ+
)∪(2kπ+
,2kπ+
],k∈Z.
则有:△=4(cosθ+1)2-4cos2θ=4+8cosθ>0,可得:cosθ>-
| 1 |
| 2 |
则有:α+β=-
| b |
| a |
故有(α+β)2=α2+β2+2αβ=4(cosθ+1)2=4cos2θ+8cosθ+4,
故:α2+β2=2cos2θ+8cosθ+4
∵|α-β|≤2
| 2 |
故α2+β2-2αβ=2cos2θ+8cosθ+4-2cos2θ=8cosθ+4≤8
从而得:cosθ≤
| 1 |
| 2 |
故:-
| 1 |
| 2 |
| 1 |
| 2 |
故θ的范围为:[2kπ+
| π |
| 3 |
| 2π |
| 3 |
| 4π |
| 3 |
| 5π |
| 3 |
点评:本题主要考察了三角函数中的恒等变换应用,根与系数的关系,属于中档题.

练习册系列答案
相关题目
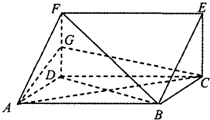 已知三棱柱ADF-BCE中,DF⊥平面ABCD,AD=DC,G是DF的中点
已知三棱柱ADF-BCE中,DF⊥平面ABCD,AD=DC,G是DF的中点